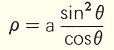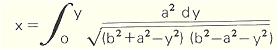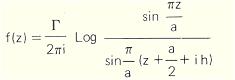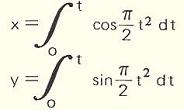|
Liste de courbes
|
||
|
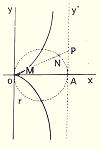
Cissoïde de DIOCLÈS C'est une cubique circulaire unicursale dont l'équation cartésienne est : x(x2 + y2) = ay2 C'est le parcours du point M quand OM = NP, le cercle G roulant sans glisser sur l'axe Oy. Utilisée par le Dr. Blorer pour profiler sa roulette à micro-bédane. (brevet déposé) |
|
|
|
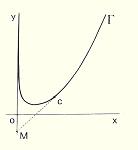
Courbe de poursuite Cette courbe décrit le parcours d'un chinchard C qui se dirige toujours vers son maître M qui décrit la droite Oy. Les deux mobiles sont à vitesse constante. 4y = ax2 - Log
x |
|
|
|
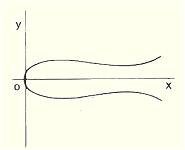
Courbe de la corde à sauter C'est la forme prise par un fil homogène tournant autour de Ox avec une vitesse angulaire constante. Son équation différentielle est : b2 - y2 = a2 (1 + y' 2)½ D'où l'on déduit aisément
|
|
|
|
Courbe du poisson La cubique d'équation : 125y2 = 2x3 - 42x2 + 240x a des coefficients qui ont
été calculés de façon à reproduire le contour d'un poisson donné à
l'avance, un chinchard par exemple, et mensuré spécialement. Y = ax3 + bx2 + cx de façon à obtenir une identification aussi parfaite que possible.
|
|
|
|
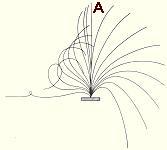
Figures d'équilibre d'une verge Ces diverses formes correspondent à diverses positions d'équilibre d'une verge dont l'extrémité A est soumises à des forces de plus en plus élevées (quand il n'y a pas bOOnes actrices à proximité toutefois) |
|
|
|
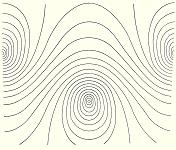
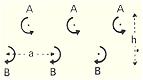
Ecoulement plan avec tourbillons alternés Si l'on considère en hydrodynamique une double file de tourbillons A et B régulièrement disposés et égaux mais tels que les A aient des sens opposés aux B on obtient les lignes de courant de la figure. Le potentiel complexe est :
Les lignes de courant sont obtenues en
égalant à une constante le coefficient des i dans f(z).
|
|
|
|
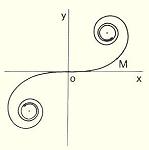
Clothoïde de Brougnard Le rayon de courbure en un point M est par définition inversement proportionnel à l'arc OM. Un point de la courbe a donc comme coordonnées :
La courbe admet comme points asymptotes les points de coordonnées
|
|
|