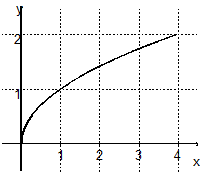Activité 1.
Proposer une formule, un intervalle
d'étude et compléter le tableau de variation pour
chacune des fonctions tracées ci-dessous.
|
f(x) = x3
sur [-2 ; 2]
|
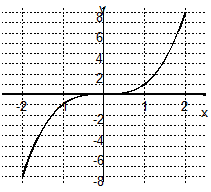
f(x) = x2
sur [-2 ; 2]
|
f(x) =
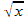sur [0 ; 2]
|
|
|
|
|
|
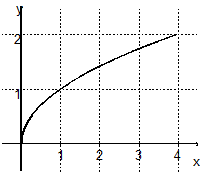
x
|
–2
|
|
2
|
|
f
|
–8
|
|
8
|
|
|
x
|
–2
|
|
0
|
|
2
|
|
f
|
4
|
|
0
|
|
4
|
|
|
x
|
0
|
|
4
|
|
f
|
0
|
|
2
|
|
Parmi les trois fonctions décrites
ci-dessus dire laquelle est paire, laquelle est impaire et laquelle
n'est ni paire ni impaire.
Fonction
paire : f(x) = x2 sur [-2 ; 2]
Fonction
impaire : f(x) = x3 sur [-2 ; 2]
Fonction
ni paire ni impaire : f(x) =
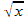sur [0 ; 2]
Activité 2.
|
Etude de la fonction f(x) = 2x2 sur [-2 ;2]
|
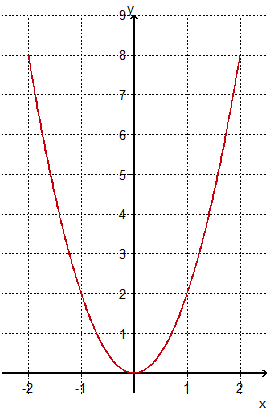
Etude de la fonction f(x) = 0,5x2 sur [-2 ; 2]
|
|
Tableau de valeurs :
|
x
|
-2
|
-1
|
0
|
1
|
2
|
|
f(x)
|
8
|
2
|
0
|
2
|
8
|
|
Tableau de valeurs :
|
x
|
-2
|
-1
|
0
|
1
|
2
|
|
f(x)
|
2
|
0,5
|
0
|
0,5
|
2
|
|
|
Représentation graphique :
|
Représentation graphique :
|
|
Tableau de variation
|
Tableau de variation
|
|
x
|
–2
|
|
0
|
|
2
|
|
f
|
8
|
|
0
|
|
8
|
|
|
x
|
–2
|
|
0
|
|
2
|
|
f
|
2
|
|
0
|
|
2
|
|
|
Parité : Fonction
paire
|
Parité : Fonction
paire
|
|
Conclusion : Les
deux fonctions sont de la forme f(x) = ax2
avec « a » positif. On remarque que les
variations sont identiques. On remarque aussi que lorsque a est
petit, la courbe est plus « évasée ».
|
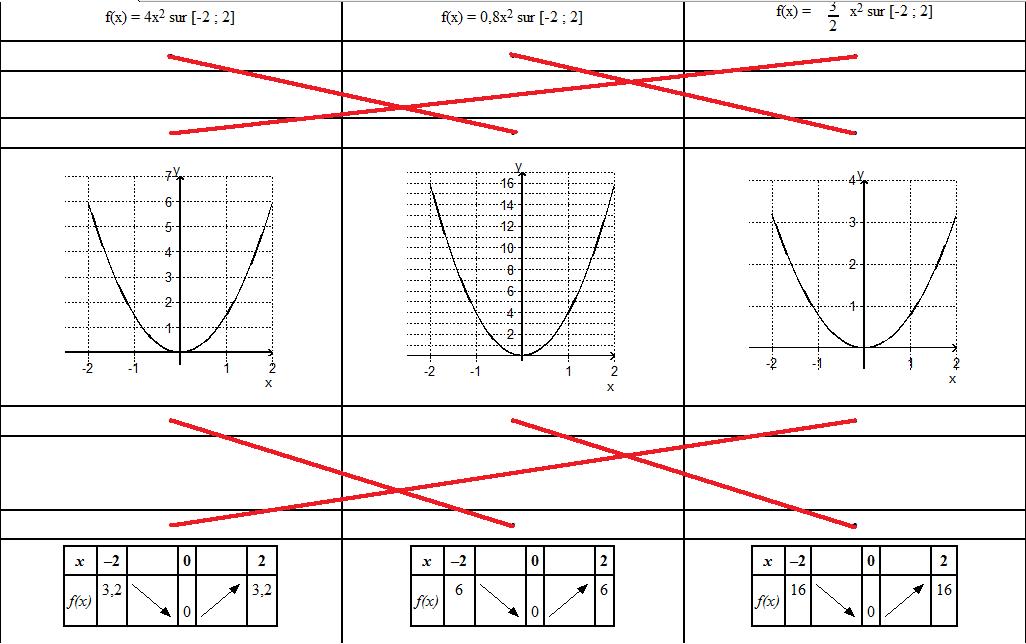
Exercice.
Relier les formules aux graphiques et
aux tableaux de variation.
Activité 3.
À l'aide du logiciel :
compléter les tableaux de variation et écrire un petit
commentaire.
|
fonction
|
Tableau de variation
|
commentaire
|
|
f(x) = x2 sur [-3 ; 3]
|
|
x
|
–3
|
|
0
|
|
3
|
|
f
|
9
|
|
0
|
|
9
|
|
« Fonction
carrée »
|
|
f(x) = 3x2 sur [-3 ; 3]
|
|
x
|
–3
|
|
0
|
|
3
|
|
f
|
27
|
|
0
|
|
27
|
|
« Fonction
carrée plus grande »
|
|
f(x) = -3x2 sur [-3 ; 3]
|
|
x
|
–3
|
|
0
|
|
3
|
|
f
|
–27
|
|
0
|
|
27
|
|
« La
précédente mais retournée »
|
|
f(x) = 0,25x2 sur [-3 ; 3]
|
|
x
|
–3
|
|
0
|
|
3
|
|
f
|
2,25
|
|
0
|
|
2,25
|
|
« Fonction
carrée plus évasée »
|
|
f(x) = -0,25x2 sur [-3 ; 3]
|
|
x
|
–3
|
|
0
|
|
3
|
|
f
|
–0,25
|
|
0
|
|
–0,25
|
|
La précédente mais retournée
|
|
Conclusion : Les
fonctions ci-dessus sont de la forme f(x) = ax2
avec « a » positif ou négatif. Si
« a » est négatif alors les
variations sont contraires à celles de la fonction carrée
|