=
=
=
=
3
" 3 " est appelé coefficient de
proportionnalité.Introduction.
Voir les activités sur http://mapage.noos.fr/hebrard/
A retenir.
Pour prouver que deux suites sont proportionnelles.
Les deux suites {2 ; 4 ; 7 ; 24 ; ...} et {6 ; 12 ; 21 ; 72 ; ...} sont proportionnelles puisqu'on a les égalités :
=
=
=
=
3
" 3 " est appelé coefficient de
proportionnalité.
Pour calculer un terme d'une suite de nombres proportionnels.
Si on passe d'une suite A à une
suite B en multipliant par 8 alors on passe de B à A en
multipliant par
|
↓ |
← |
A |
2 |
3 |
5 |
← |
↑ |
|
*8 |
|
|
|
|
*0,125 = (1/8) |
||
|
|
|
|
|
||||
|
↓ |
→ |
B |
16 |
24 |
40 |
→ |
↑ |
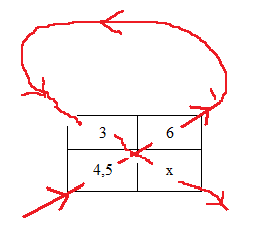
Pour calculer la quatrième proportionnelle.
On peut utiliser le « produit en croix ».
|
3 |
6 |
|
4,5 |
x |
Pour calculer x on fait :
=
9 donc x = 9
On appelle cette méthode le produit en croix :
Pour représenter graphiquement deux suites de nombres proportionnels.
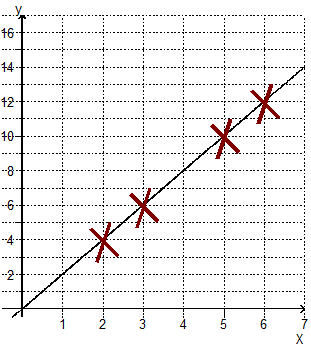
Si la suite des nombres représentant les abscisses est proportionnelle à la suite des nombres représentant les ordonnées, alors les points tracés dans le repère sont alignés sur une droite.
Cette droite passe par l'origine du repère.
|
X |
2 |
3 |
5 |
6 |
|
Y |
4 |
6 |
10 |
12 |
CH Page