Galilée et les poissons rouges

J’ai raconté deux fois la vie d’Einstein. Je lui ai aussi consacré une petite “dramatique” radiophonique, diffusée sur France-Culture.
Quand on fréquente Einstein, on rencontre forcément Galilée. En effet, le mot “relativité” a été inventé par Poincaré pour décrire la théorie du mouvement de Galilée. Einstein a modifié un peu cette théorie dans un article intitulé “Électrodynamique des corps en mouvement”. Max Planck, qui a publié l’article, trouvait le titre fastidieux à prononcer (surtout en allemand). Il disait plus volontiers “la relativité d’Einstein” en référence à celle de Galilée. Einstein lui-même trouvait l’usage du mot relativité mal adapté à sa théorie. Il aurait préféré l’expression “principe d’invariance”.
Bref, j’ai rencontré Galilée et je l’ai trouvé intéressant et sympathique. J’ai décidé de mieux le connaître et j’ai fini par raconter sa vie.

Livre publié par Le Pommier en mai 2010.
180 pages.

Que viennent faire des poissons rouges dans le titre?

Copernic avait tiré de l’oubli une hypothèse connue dès l’antiquité grecque: ce n’est pas le soleil qui tourne, c’est la terre. Quand Galilée a regardé le ciel à travers une lunette en 1609, il a découvert que la planète Vénus avait des phases comme la lune, ce qui s’accordait bien avec l’hypothèse de Copernic. Encore fallait-il répondre à une objection déjà formulée par Aristote: si la terre tournait vraiment à plus de 1000 km/h (trente mille kilomètres environ, à la latitude de Florence, en vingt-quatre heures), nous aurions du mal à rester debout et les feuilles tomberaient à dix kilomètres des arbres, etc.
Galilée donne l’exemple suivant pour montrer que le mouvement est toujours relatif, c’est-à-dire que le mouvement d’un bateau ou de la terre ne nous affecte pas.
“Enfermez-vous avec quelques amis dans une cabine sous le pont d’un grand navire. Vous y aurez placé un aquarium rempli d’eau où nagent quelques poissons, une grande cage contenant des papillons et des petits oiseaux, un petit seau suspendu au plafond dont l’eau coule goutte à goutte dans une bouteille. Quand le navire est immobile, observez comment les oisillons volent dans toutes les directions avec la même vitesse, comment les poissons nagent indifféremment dans un sens et dans l’autre, comment les gouttes tombent toutes dans le vase. Si vous jetez une balle à votre ami, l’effort est le même où qu’il soit placé. Si vous sautez à pieds joints, vous franchirez le même espace dans une direction que dans une autre. Ensuite, demandez au capitaine de mouvoir le navire à n’importe quelle vitesse, à condition que le déplacement soit uniforme, sans balancement, et suive une ligne droite. Vous ne constaterez aucun changement dans les effets observés auparavant. Aucune observation ne vous permet de savoir si le navire est immobile ou se meut.”
Aujourd’hui on imaginerait plutôt un voyage en avion ou en TGV. Nous marchons aussi facilement vers l’avant que vers l’arrière du train. Nous ne sentons pas qu’il avance à 300 km/h.

L’exemple des poissons rouges qui ne perçoivent pas le mouvement du bateau montre que la terre peut bouger tout en nous paraissant immobile.
Pour expliquer comment une chose aussi étrange est possible, Galilée doit réinventer le mouvement.
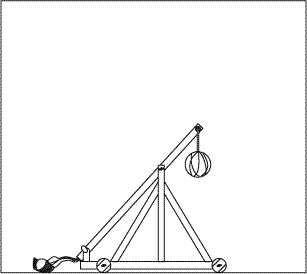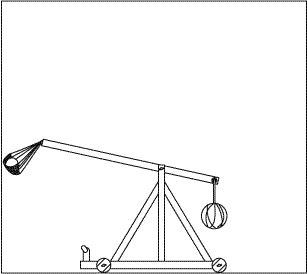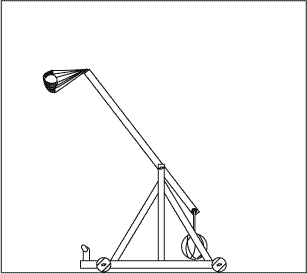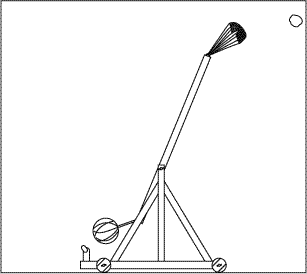
Selon Aristote (dont la pensée a encore force de loi au temps de Galilée), les objets sont paresseux et ne souhaitent qu’une chose: l’immobilité. Ils bougent seulement quand une force extérieure les pousse. Par exemple, le boulet de la catapulte monte parce que la nacelle le soulève.
Merveille de la technologie moderne: approchez la souris de la catapulte et maintenez-la dans le cadre pour animer l'image. [J’ai dit souris: cette animation ne fonctionne pas bien sur une tablette. Idem pour les suivantes.]
Aristote voit bien que le boulet continue à bouger quand la nacelle cesse de le propulser. C’est qu’il déplace des particules d’air, dit-il, qui veulent revenir à leur place pour se reposer. Ce faisant, elles poussent le boulet. Il va déranger d’autres particules, qui le poussent à leur tour, et ainsi de suite.
Dès le Moyen-Âge, des petits malins remarquent que les particules d’air peuvent pousser un boulet dodu, mais qu’on les imagine mal poussant un javelot pointu en ses deux extrémités.
Galilée inverse l’hypothèse d’Aristote. Pour lui, la paresse des objets les empêche de modifier leur comportement. Quand ils bougent, ils continuent à bouger. Quand ils sont immobiles, ils restent immobiles. Cette paresse des objets porte aujourd’hui un nom technique: l’inertie.
Soulevé par la nacelle, le boulet acquiert ce qu’on appelle une “quantité de mouvement". Quand la nacelle cesse de le propulser, il conserve cette quantité de mouvement. On nomme “principe d’inertie” cette conservation. Le boulet ralentit parce que les molécules d’air, loin de l’aider à avancer, le freinent peu à peu.
Imaginons une catapulte sur la lune, où il n’y a pas d’air. Selon Aristote, en l’absence de particules d’air pour pousser le boulet, il tombe à la verticale dès que la nacelle le relâche. Selon Galilée, il va beaucoup plus vite et plus loin dans le vide que dans l’air. Il finit par tomber au sol à cause de la pesanteur, comme sur terre.

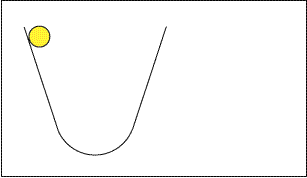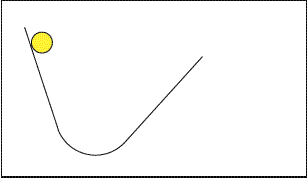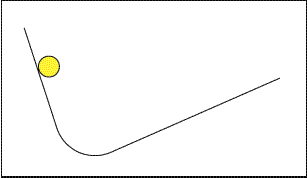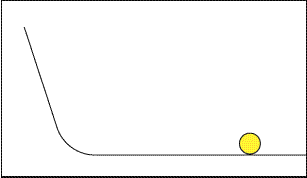
Les textes d’Aristote étaient à peu près aussi sacrés que les Évangiles. Si c’était écrit dans Aristote, c’était forcément vrai. Galilée n’a pas peur de s’attaquer aux dogmes. Comment décider si un objet en mouvement préfère continuer à bouger ou s’arrêter pour se reposer? “Il suffit d’essayer”, dit Galilée. Il invente la méthode expérimentale. L'image ci-contre illustre l’une de ses expériences, qui utilise deux plans inclinés. Les virtuoses du skateboard font des acrobaties sur des dispositifs analogues.
La boule remonte presque à sa hauteur initiale. La différence est due au frottement des plans inclinés, qui la ralentit un peu. Si on abaisse le second plan incliné, la boule remonte toujours à la même hauteur, donc elle parcourt une distance plus grande. Quand le second plan devient horizontal, la boule va au bout du monde – ou plutôt, irait au bout du monde si le frottement ne finissait par l’arrêter. Approchez la souris et maintenez-la dans le cadre pour voir une animation représentant l’ensemble de l’expérience.
Galilée prouve ainsi le principle d’inertie: la boule conserve sa quantité de mouvement et continue indéfiniment à bouger.

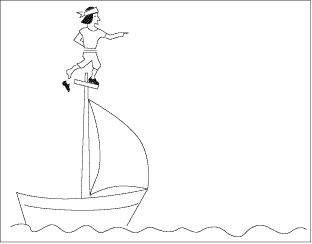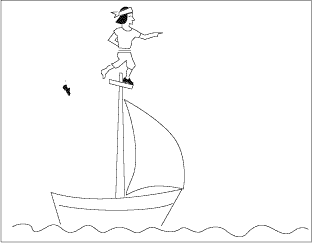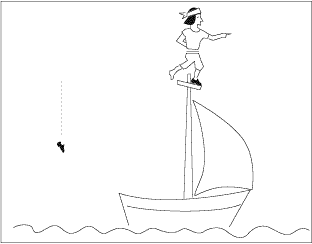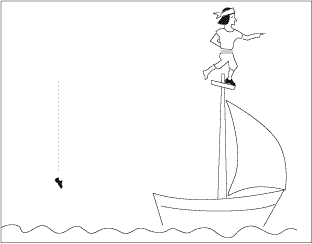
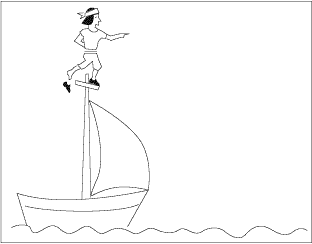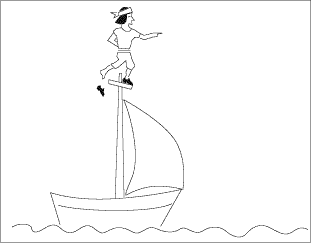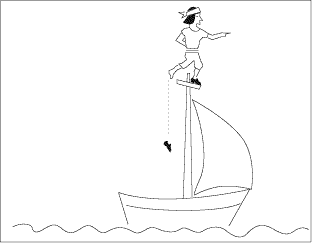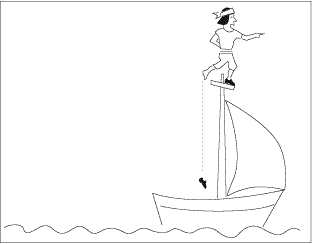
Encore une histoire de bateau.
Pour les gens qui suivent Aristote à la lettre, la chaussure cesse d’être poussée horizontalement quand elle quitte le pied du marin. Elle n‘avance plus alors que le marin continue d’avancer. Résultat, elle ne tombe pas au pied du mât, comme elle le ferait si le bateau était immobile, mais loin derrière. C’est ce qui se passe si vous approchez la souris de l’image du haut.
Galilée se moque des imbéciles qui prétendent que la chaussure tombe dans la mer. “Avez-vous essayé?" leur demande-t-il. La chaussure a acquis une certaine quantité de mouvement horizontal. Quand elle quitte le pied du marin, elle conserve cette quantité de mouvement (selon le principe d’inertie et continue à avancer à l’horizontale en même temps que le bateau. Elle tombe donc le long du mât et s’arrête au pied du mât. Passez la souris sur l’image du bas pour voir ce qui se passe en réalité.
La réalisation de cette expérience est une autre manière de prouver le principe d’inertie.

L’illustration ci-contre illustre un sujet qui n’a pas de rapport avec le mouvement de la terre: la pesanteur. La Bible n’en parle pas, donc Galilée n’offense pas l’Église en l’abordant. Il commet tout de même un nouveau crime de lèse-majesté puisqu’il s’attaque une fois de plus à Aristote.
Pour le philosophe grec, les objets lourds tombent plus vite que les objets légers. Un objet deux fois plus lourd qu’un autre tombe deux fois plus vite.
Galilée pense – et démontre – que tous les objets tombent à la même vitesse. C’est très facile: il suffit de monter en haut de la tour de Pise et de laisser tomber un boulet de canon et une balle d’arquebuse. Selon Aristote, si on suppose le boulet dix fois plus lourd que la balle, celle-ci n’a pas le temps de parcourir un étage que déjà le boulet touche le sol.
Approchez la souris et maintenez-la dans le cadre pour voir ce qui pourrait se passer si Aristote avait raison.
Le dernier élève et premier biographe de Galilée a raconté que son maître était monté sur la tour pour réaliser cette expérience. Les biographes d’aujourd’hui doutent qu’il ait pris la peine de monter là-haut. Il s’est contenté d’une démonstration théorique: si on coupe le boulet en deux moitiés attachées par une ficelle, descendra-t-il deux fois moins vite? Et si on enlève la ficelle?