LA MESURE DE LA CIRCONFERENCE DE LA TERRE PAR ERATOSTHENE
Sur les pas d'Eratosthène.
Eratosthène a estimé le périmètre de la Terre, d'après
son expérience, égal à 250.000 stades attiques (44250 km.) à savoir avec
une approximation de 10% par rapport à la valeur réelle. Lorsqu'on pense
que le seul instrument utilisé a été un bâton (gnômon) à une époque où pratiquement
tout le monde croyait que la Terre est un disque plat, il y a de quoi rester
admiratif devant la force de l'esprit humain.
Avertissement : la traduction ci-dessous est un
travail collectif réalisé par les hellénistes du forum, pour la plupart sous
leur pseudonyme, news:fr.lettres.langues-anciennes.grec : Chaeréphon, Robin Delisle alias Anaxagore, Périclès, Iulius, Rob, Lucien de Luca et André Charbonnet . Le texte provient de Greek Mathematics édité par Loeb University Press - Classical library -
Harvard University Press mais il s'agit en fait d'un passage du livre de
Cléomède De motu circulari corporum coelestium
écrit au 1° siècle ap JC. Chaeréphon propose sa propre traduction, plus littéraire, sur la base du texte édité par le TLG (Thesaurus Linguae Graecae).
Καὶ ἡ μὲν τοῦ Ποσειδωνίου ἔφοδος πρεὶ τοῦ κατὰ τὴν γῆν μεγέθους
τοιαύτη, ἡ δὲ τοῦ Ἐρατοσθένους γεωμετρικῆς ἐφοδοῦ ἐχομένη, καὶ
δοκοῦσα τι ἀσαφέσετερον ἔχειν. ποιήσει δὲ σαφῇ τὰ λεγόμενα ὑπ’ αὐτοῦ
τάδε προῦποτιθεμένων ἡμῶν. ὑποκείσθω ἡμῖν πρῶτον μὲν κῶ?αῦθα ,
ὑπὸ τῷ μεσημβρινῷ κεῖσθαι Συήνην καὶ Ἀλεξάνδρειαν, καὶ δεύτερον, τὸ
διάστημα τό μεταξὺ τῶν
πόλεων πεντακισχιλίων σταδίων εἶναι, καὶ
τρίτον, τὰς καταπεμπομένας ἀκτῖνας ἀπὸ διαφόρων μερῶν τοῦ ἡλίου ἐπὶ
διάφορα τῆς γῆς μέρη παραλλήλους εἶναι· οὗτως γὰρ ἔχειν αὐτὰς οἱ
γεωμέτραι ὑποτίθενται.
Et la méthode de Posidonios à propos de la grandeur de la terre est
de cette sorte, mais celle d'Eratosthène est dépendante d'une
méthode géométrique et semble avoir quelque chose de moins clair. Il
rendrait claires ce qu'il a dit si nous les présupposons au
préalable. Qu'il soit admis pour nous, premièrement là-même(?) que
Syène et Alexandrie sont établies sous le méridien, deuxièmement que
la distance entre les deux cités est de 5000 stades, troisièmement
que les rayons envoyés de différents endroits du soleil sur
différents endroits de la Terre sont parallèles ; en effet, les
géomètres supposent qu'il en est ainsi.
Τέταρτον ἐκεῖνο ὑποκείσθω, δεικνὺμενον παρὰ τοῖς γεωμέτραις, τὰς εἰς
παραλλήλους ἐμπιπτούσας εὐθείας τὰς ἐναλλὰξγωνίας ἴσας ποιεῖν*,
πέμπτον,τὰς ἐπὶ ἴσων γωνιῶν βεβηκυίας περιφερείας ὁμοίας εἶναι,
τουτἐστι τὴν αὐτὴν ἀναλογίαν καὶ τὸν αὐτὸν λόγον ἔχειν πρὸς τοὺς
οἰκείους κύκλους,δεικνυμένου καὶ τούτου παρὰ τοῖς γεωμέτραις. Ὁπόταν
γὰρ περιφέρειαι ἐπὶ ἴσων γωνιῶν βεβηκυῖαι, ἄν μία ἡτισοῦν αὐτῶν
δέκατον ᾖ μέρος τοῦ οἰκείου κύκλου, καὶ αἱ λοιπαὶ πᾶσαι δέκατα μέρη
γενήσονται τῶν οἰκείων κύκλων.
Quatrièmement que ceci soit admis comme démontré auprès des
géomètres, que les droites sécantes des parallèles forment des
angles alternes égaux, cinquièmement que les arcs de cercle qui
reposent sur des angles égaux sont semblables, c'est à dire
qu'ils ont la même similitude et le même rapport relativement aux
cercles correspondants,ceci étant démontré aussi chez les
géomètres.
Lorsqu'en effet les arcs de cercle reposent sur des angles égaux,
quelque soit l'un (d'entre-eux) s'il est la dixième partie de son
propre cercle, tous les autres seront les dixièmes parties de leurs
propres cercles.
**
Τούτων ὁ κατακρατήσας οὐκ ἄν χαλεπῶς τὴν ἔφοδον τοῦ Ἐρατοσθένους
καταμάθοι ἔχουσαν οὔτως. ὑπὸ τῷ αὐτῷ κεῖσθαι μεσημβρινῷ φησι Συήνην
καὶ Ἀλεξάνδρειαν. ἐπεὶ οὖν μέγιστοι τῶν ἐν τῷ κόσμῳ οἱ μεσημβρινοί,
δεῖ καὶ τοὺς ὑποκειμένους τούτοις τῆς γῆς κύκλους μεγίστους εἶναι
ἀναγκαίως. Ὤστε ἡλικον ἄν τὸν διὰ Συήνης καὶ Ἀλεξανδρείας ἥκοντα
κύκλον τῆς γῆς ἡ ἔφοδος ἀποδείξει αὕτη, τηλικοῦντος καὶ ὁ μέγιστος
ἔσται τῆς γῆς κύκλος. Φησὶ τοίνυν, καὶ ἔχει οὕτως, τὴν Συήνην ὑπὸ τῷ
θερινῷ τροπικῷ κεῖσθαι κύκλῳ. Ὁπόταν οὖν ἐν καρκίνῳ γενόμενος ὁ
ἥλιος καὶ θερινὰς ποιῶν τροπὰς ἀκριβῶς μεσουρανήσῃ, ἄσκιοι γινονται
οἱ τῶν ὡρολογίων γνώμονες ἀναγκαίως, κατὰ κάθετον ἀκριβῇ τοῦ ἡλίου
ὑπερκειμένου · καὶ τοῦτο γίνεσθαι λόγος ἐπὶ σταδίους τριακοσίους τὴν
διάμετρον.
Celui qui pourrait se prévaloir de ces faits comprendrait sans
difficulté le cheminement d'Eratosthène qui tient en ceci : il
affirme que Syène et Alexandrie se tiennent sous le même méridien.
Et puisque les méridiens sont les plus grands de ceux qui sont dans
l'univers, il faut nécessairement que les cercles terrestres qui
sont placés sous eux soient aussi les plus grands. De sorte que ce
cheminement démontre qu'un cercle de la terre allant de Syène à
Alexandrie serait aussi grande que la Terre elle-même, et que le
plus grand de même taille sera aussi un cercle de la Terre. Il dit
aussi, et il en est ainsi, que Syène est située sous le tropique de
l'été. Lorsque donc, le soleil étant dans la constellation du
cancer, faisant exactement le solstice d'été est au milieu du ciel,
les gnomons des cadrans solaires sont nécessairement sans ombres, le
soleil se situant exactement à la verticale ; et c'est notoire sur un diamètre de 300 stades.
Ἐν Ἀλεξανδρείᾳ δὲ τῇ αὐτῇ ὥρᾳ ἀποβάλλουσιν οἱ τῶν ὡρολογίων γνώμονες
σκίαν, ἅτε πρὸς ἄρκτῳ μᾶλλον τῆς Συήνης ταύτης τῆς πόλεως κειμένης.
Ὑπὸ τῷ αὐτῷ μεσημβρινῷ τοίνυν καὶ μεγίστῳ κύκλῳ τῶν πόλεων κειμένων,
ἄν περιαγάγωμεν περιφέρειαν ἀπὸ τοῦ ἄρκου τῆς τοῦ γνώμονος σκιᾶς ἐπὶ
τὴν βάσιν αὐτὴν τοῦ γνώμονος τοῦ ἐν Ἀλεξανδρείᾳ ὡρολογίου, αὕτη ἡ
περιφέρεια τμῆμα γενήσεται τοῦ μεγίστου τῶν ἐν τῇ σκάφῃ κύκλων, ἐπεὶ
μεγίστῳ κύκλῳ ὑπόκειται ἡ τοῦ ὡρολογίου σκάφη. Εἰ οὖν ἑξῆς νοήσαιμεν
εὐθείας διὰ τῆς γῆς ἐκβαλλομένας ἀφ’ ἑκατέρου τῶν γνωμόνων, πρὸς τῷ
κέντρῳ τῆς γῆς συμπεσοῦνται.
A Alexandrie à cette heure-là, les gnomons des cadrans solaires
projettent une ombre, puisque cette ville est située davantage vers
le nord que Syène. Ces deux villes étant sous le même méridien et le
plus grand cercle, si nous conduisons un arc de cercle à partir de
l'extrémité de l'ombre du gnomon jusqu'à la base même du gnomon du
cadran solaire qui se trouve à Alexandrie, ce même arc-de-cercle
sera une section du plus grand des cercles du cadran, puisque la cavité du cadran se situe sous le plus grand cercle. Si
donc ensuite, nous nous représentons des droites passant par la
Terre à partir de chacun des gnomons, elles se rejoindront près du
centre de la Terre.
ἐπεὶ οὖν τὸ ἐν Συήνῃ ὡρολόγιον κατὰ κάθετον ὑπόκειται τῷ ἡλίῳ, ἄν
ἐπινοήσωμεν εὐθεῖαν ἀπὸ τοῦ ἡλίου ἥκουσαν ἐπ’ ἄκρον τὸν τοῦ
ὡρολογίου γνώμονα, μία γενήσεται εὐθεῖα ἡ ἀπὸ τοῦ ἡλίου μέχρι τοῦ
κέντρου τῆς γῆς ἥκουσα. ἐὰν οὖν ἑτέραν εὐθεῖαν νοήσωμεν ἀπὸ τοῦ
ἄκρου τῆς σκιᾶς τοῦ γνώμονος δι’ἄκρου τοῦ γνώμονος ἐπὶ τὸν ἥλιον
ἀναγομένην ἀπὸ τῆς ἐν Ἀλεξανδρείᾳ σκάφης, αὕτη καὶ ἡ προειρημένη
εὐθεῖα παράλληλοι γενήσονται ἀπὸ διαφόρων γε τοῦ ἡλίου μερῶν ἐπὶ
διάφορα μέρη τῆς γῆς διήκουσαι. Εἰς ταύτας τοίνυν παραλλήλους οὔσας
ἐμπίπτει εὐθεῖα ἡ ἀπὸ τοῦ κέντρου τῆς γῆς ἐπὶ τὸν ἐν Ἀλεξανδρείᾳ
γνώμονα ἥκουσα, ὥστε τὰς ἐναλλὰξ γωνίας ἴσας ποιεῖν · ῷν ἡ μέν ἐστι
πρὸς τῷ κέντρῳ τῆς γῆς κατὰ σύμπτωσιν τῶν εὐθειῶν, αἵ ἀπὸ τῶν
ὠρολογίων ἤχθησαν ἐπὶ τό κέντρον τῆς γῆς, γινομένη, ἡ δὲ κατὰ
σύμπτωσιν ἄκρου τοῦ ἐν Ἀλεξανδρείᾳ γνώμονος καὶ τῆς ἀπ’ἄκρου τῆς
σκιᾶς αὐτοῦ ἐπὶ τὸν ἥλιον διὰ τῆς πρὸς αὐτον ψαύσεως ἀναχθείσης
γεγενημενὴ.
Lorsque donc le cadran solaire de Syène est à la verticale sous le soleil,
si nous imaginons une ligne droite venant du soleil jusqu'au sommet du gnomon
du cadran, il en résultera une ligne droite venant du soleil jusqu'au centre
de la Terre. Si nous imaginons une autre ligne droite à partir de l'extrémité
de l'ombre du gnomon (et) reliant le sommet du gnomon du cadran concave d'
Alexandrie au soleil, cette dernière ligne et la ligne qui précède seront
parallèles, reliant différents points du Soleil à différents points de la
Terre. Sur ces droites donc , qui sont parallèles, tombe une droite qui va
du centre de la terre jusqu'au gnomon d' Alexandrie, de manière à créer des
angles alternes égaux; l'un d'eux se situe au centre de la Terre à l'intersection
des lignes droites qui ont été tirées des cadrans solaires jusqu'au centre
de la Terre, l'autre se trouve à l'intersection du sommet du gnomon d'Alexandrie
et de la droite tirée de l'extrémité de son ombre jusqu'au soleil, à son
point de contact avec le gnomon.
Καὶ ἐπὶ μὲν ταύτης βέβηκε περιφέρεια ἡ ἀπ’ ἄκρου τῆς σκιᾶς τοῦ
γνώμονος ἐπὶ τὴν βάσιν αὐτοῦ περιαχθεῖσα, ἐπὶ δὲ τῆς πρὸς τῷ κέντρῳ
τῆς γῆς ἡ ἀπο Συήνης διὴκουσα εἰς Ἀλεξάνδρειαν. Ὅμοιαι τοίνυν αἱ
περιφέρειαί εἰσιν ἀλλήλαις ἐπ’ ἴσων γε γωνιῶν βεβηκυῖαι. Ὃν ἄρα
λόγον ἔχει ἡ ἐν τῇ σκάφῃ πρὸς τὸν οἰκεῖον κύκλον, τοῦτον ἔχει τὸν
λόγον καὶ ἡ ἀπὸ ἀπο Συήνης εἰς Ἀλεξάνδρειαν ἤκουσα. Ἡ δέ γε ἐν τῇ
σκάφῃ πεντηκοστὸν μέρος εὑρίσκεται τοῦ οἰκείου κύκλου. Δεῖ οὖν
ἀναγκαίως καὶ τὸ ἀπο Συήνης εἰς Ἀλεξάνδρειαν διάστημα πεντηκοστὸν
εἶναι μέρος τοῦ μεγίστου τῆς γῆς κύκλου · καὶ ἐστι τοῦτο σταδίων
πεντακισχιλίων. ὁ ἄρα σύμπας κύκλος γίνεται μυριάδων εἴκοσι πέντε.
καὶ ἡ μὲν Ἐρατοσθένους τοιαύτη.
Et sur cet angle s'appuie l'arc de cercle qui fait le tour de la
pointe de l'ombre du gnomon jusqu'à sa base tandis que celui qui est
proche du cente de la terre s'appuie l'arc qui va de Syène à
Alexandrie. Ces arcs de cercle sont donc semblables l'un à l'autre
en s'appuyant sur des côtés égaux. Le rapport qu'a l'arc du cadran
avec son propre cercle, l'arc qui va de Syène à Alexandrie a ce
rapport aussi. Mais on trouve que l'arc du cadran est la
cinquantième partie de son propre cercle. Il faut donc
nécessairement que la distance qui va de Syène à Alexandrie soit la
cinquantième partie du plus grand cercle de la Terre. Et elle est de
5000 stades. Le cercle dans sa totalité fait donc 250 000 stades.
Voilà la méthode d'Eratosthène.
* Vingt-septième proposition du livre premier des Eléments d'Euclide
Ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐναλλὰξ γωνίας ἴσας ἀλλήλαις ποιῇ, παράλληλοι ἔσονται ἀλλήλαις αἱ εὐθεῖαι.
Quand un droite sécante de deux droites forme deux angles alternes égaux
l'un à l'autre, les droites sont parallèles l'une de l'autre.
** Les angles dont il est question dans le texte sont les angles
POS et BPO.
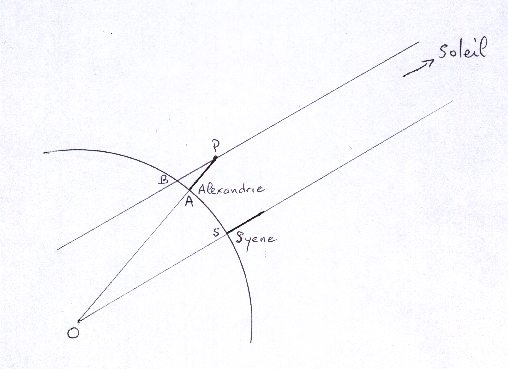
Eratosthène a remarqué que lorsque le soleil est à la verticale
du cadran solaire de Syene, l'angle BPA formé par
la tige AP du cadran d'Alexandrie avec la droite qui joint
l'extrémité de cette tige à l'extrémité de son ombre est
égal à l'angle dont on voit l'arc joignant Alexandrie à Syene
depuis le centre de la terre, ce qui ensuite connaissant la distance
d'Alexandrie à Syene donnera avec une simple règle de trois la
circonférence de la terre.
*** Remarques sur la σκάφη
Je me demande pourquoi, dans le texte
traduit par Anaxagore, on parle d'une
σκάφη pour le cadran solaire situé à
Alexandrie. Le mot peut signifier fouille,
ou n'importe quel récipient creux (vase,
pétrin...), tandis que le cadran solaire
est plan. Je suggère l'explication suivante :
Eratosthène avait besoin de mesurer l'angle
formé par la tige ( γνώμων) avec le rayon
reliant son extrémité à l'extrémité de
son ombre. Aujourd'hui n'importe quel
lycéen saurait le faire, en divisant la
longueur de l'ombre par celle de la tige,
le quotient étant la tangente de l'angle.
Mais les Grecs ne connaissaient pas la
trigonométrie, il fallait que tout calcul
soit réduit à la géométrie euclidienne.
Alors Eratosthène a fabriqué un cadrant
en creux, représentant la surface d'une
sphère de rayon égal à la longueur du
gnômôn, ayant comme centre son
extrémité. En traçant sur ce cadran de
graduations, représentant les fractions
d'un cercle complet, on peut lire
immédiatement l'angle à l'extrémité
de l'ombre.
Eratosthène l'a estimé égal à 1/50 ème
du cercle (toujours la manie grecque
pour les nombres rationnels !)
à savoir 7,2 degrés.
Quelqu'un aurait-il une autre explication ?
Traduction proposée par Chaeréphon :
Voilà quelle est la méthode de Posidonios à propos de la grandeur de la Terre;
celle d'Eratosthène est dépendante d'une méthode géométrique et, à mon avis,
est un peu plus opaque. Cela rendra clair ce qu'il dit si nous posons comme
préalable ce qui suit. Admettons comme préalable, premièrement et hic et
nunc que Syène et Alexandrie sont situées sur le même méridien, deuxièmement
que la distance entre les deux villes est de 5000 stades, troisièmement que
les rayons envoyés de différents points du Soleil sur différents points de
la Terre sont parallèles -- en effet, les géomètres admettent comme préalable
qu'il en est ainsi. Quatrièmement que ceci soit admis comme démontré chez
des géomètres, que les droites sécantes de parallèles forment des angles
alternes égaux; cinquièmement que les arcs de cercles qui reposent sur des
angles égaux sont semblables, c'est-à-dire ont la même proportion et le même
rapport relativement à leurs cercles respectifs, ceci aussi étant démontré
chez les géomètres. Lorsqu'en effet des arcs de cercle reposent sur des angles
égaux, si un seul d'entre eux, quel qu'il soit, représente le dixième de
son cercle, tous les autres représenteront le dixième de leurs cercles respectifs.
Celui qui garde bien en tête ces préalables pourra sans doute sans difficulté
comprendre à fond la méthode d'Eratosthène telle qu'elle est.
Syène et Alexandrie, dit-il, sont situées sur le même méridien. Lors donc
que les méridiens sont les plus grands cercles de l'univers, il
s'ensuit nécessairement que les cercles de la Terre qui en sont la projection
sont les plus grands de la Terre. Par conséquent la grandeur
de la circonférence terrestre qui passe par Syène et Alexandrie qui sera
démontrée par cette méthode sera aussi la plus grande circonférence de la
Terre. Eratosthène dit donc, et il en est bien ainsi, que Syène se trouve
sur le tropique d'été (i.e. tropique du cancer). Lors donc que le soleil
est entré dans le Cancer et passe exactement au zénith lors du solstice d'été,
les gnomons des cadrans solaires nécessairement n'ont plus d'ombre, puisque
le soleil se trouve exactement à la verticale; et cela de se produire, à
ce qu'on dit, sur 300 stades de diamètre (= dans un rayon de 24 km.).
Mais à Alexandrie à la même heure, les gnomons des cadrans projettent une
ombre, puisque cette ville est située plus au nord que Syène. Les deux villes
étant donc situées sur le même méridien et sur la plus grande circonférence,
si nous traçons un arc de cercle à partir de
l'extrémité de l'ombre du gnomon jusqu'à la base même du gnomon du cadran
d'Alexandrie. cet arc de cercle sera une partie du plus grand des cercles
du cadran, puisque la sphère du cadran est située sous le plus grand cercle.
Si donc par la suite nous imaginons des droites traversant la Terre à partir
de chacun des gnomons, elles se couperont au centre de la Terre.
Lorsque donc le cadran solaire de Syène est à la verticale sous le Soleil,
si nous imaginons une ligne droite venant du Soleil jusqu'au
sommet du gnomon du cadran, il en résultera une ligne droite venant du Soleil
jusqu'au centre de la Terre. Si nous imaginons une autre ligne
droite à partir de l'extrémité de l'ombre du gnomon reliant le sommet du
gnomon du cadran sphérique d' Alexandrie au Soleil, cette dernière ligne
et la ligne précédente seront parallèles, puisque reliant différents points
du Soleil à différents points de la Terre. Ces droites donc, qui
sont parallèles, sont coupées par une droite qui va du centre de la Terre
jusqu'au gnomon d' Alexandrie, en formant des angles alternes
égaux; le premier se situe au centre de la Terre à l'intersection des droites
qui ont été construites des cadrans solaires jusqu'au centre de
la Terre, l'autre se trouve à l'intersection du sommet du gnomon d'Alexandrie
avec la droite construite de l'extrémité de son ombre
jusqu'au Soleil, et passant par son point de contact avec le gnomon. Sur
cet angle vient se poser un arc de cercle qui va de l'extrémité de
l'ombre du gnomon jusqu'à sa base, sur l'autre angle, dirigé vers le centre
de la Terre, l'arc de cercle qui va de Syène à Alexandrie. Dès
lors les arcs de cercle sont semblables entre eux, étant construits sur des
angles égaux. Et donc le rapport qui existe entre l'arc de cercle du
cadran sphérique et son cercle est le même pour l'arc de cercle qui va de
Syène à Alexandrie. On trouve que l'arc de cercle du cadran est la
cinquantième partie de son cercle (i.e. 7°12'). Il s'ensuit nécessairement
que la distance de Syène à Alexandrie est aussi la cinquantième partie du
grand cercle de la Terre. Cet arc de cercle est de 5000 stades. La circonférence
totale est donc de 250'000 stades. Voilà la méthode d'Eratosthène.
Il place aussi lors du solstice d'hiver des cadrans dans chacune des deux
villes; ces cadrans produisent des ombres, celle d'Alexandrie est
nécessairement plus grande puisque cette ville est plus éloignée du tropique
d'hiver (tropique du Capricorne). En considérant l'excédent d'ombre que l'on
observe entre Syène et Alexandrie, on trouve que cet excédent aussi est la
cinquantième partie du plus grand des cercles des cadrans. C'est ainsi, à
partir de ces calculs que l'on connaît que la plus grande circonférence de
la Terre est de 250'000 stades. Le diamètre de la Terre sera donc de plus
de 80'000 stades, puisqu'il faut qu'il soit le tiers du plus grand des cercles.
Ceux donc qui disent que la Terre ne peut pas être sphérique à cause des
dépressions des mers et des aspérités des montagnes le conjecturent de façon
tout à fait illogique. En effet on ne trouve pas de montagne plus haute ni
de mer plus profonde que 15 stades (2475 m.). Trente stades en regard de
plus de 80'000 stades n'ont aucun rapport (i.e. ont un rapport de zéro);
mais c'est exactement comme s' il y avait un grain de poussière sur une sphère.
Et les aspérités autour des petites boules des platanes ne les empêchent
pas d'être des petites sphères; cependant ces aspérités ont un rapport plus
important à la grandeur totale des boules que les dépressions de la mer et
les sommets des montagnes par rapport à la grandeur totale de la terre.
Commentaires et notes de Chaeréphon :
Strabon et Eratosthène :
"Ératosthène soutient que la terre habitée forme approximativement un cercle,
qui tend à se fermer sur lui-même, de sorte que, si l'immensité de l'océan
Atlantique n'y faisait obstacle, il nous serait possible d'aller par mer
d'Ibérie jusqu'en Inde: il suffirait de suivre le même parallèle, et de parcourir
la section qui reste, soit un peu plus du tiers de la circonférence totale,
en admettant une valeur inférieure à
deux cent mille stades ( env. 36000 km) pour le parallèle sur lequel a été
faite la précédente répartition depuis l'Inde jusqu'à l'Ibérie."
(Strabon I, 4, 6-7)
"Ératosthène émet encore l'hypothèse que les quelque soixante-dix mille stades
(env. 12500 km) qui représentent la longueur du monde habité valent la moitié
du cercle entier sur lequel est prise cette longueur, de sorte que, dit-il,
si, partant de l'occident, l'on naviguait par vent
d'est, au bout d'un nombre égal de stades on aborderait aux Indes."
(Strabon II, 3, 6)
Circonférence de la Terre et stades
D'après le texte de Cléomédès, la circonférence totale de la Terre calculée
par Eratosthène est de 250'000 stades. Dans le Kleine Pauly, je trouve mentionné
252'000 stades...interrogation ... (bon ça ne fait qu'une erreur de 0.79
%).
Dans deux autres ouvrages, je trouve également la mention de 252'000 stades.
Quelle était la longueur du stade ?
Le stade valait généralement 600 pieds. Mais comme les pieds variaient d'une
cité à l'autre, le stade vaut entre 179 et 213 m. Ce qui n'arrange pas nos
calculs.
A l'époque hellénistique on utilisait des stades de 165 m et de 149 m (stade des bématistes).
Selon ces derniers chiffres la circonférence du méridien d'Eratosthène vaut soit 41250 km (41580) soit 37250 km (37548).
Pour ma part je préfère garder le chiffre cité par Cléomédès, avec un stade de 165 m., soit 41250 km.
Sur la page internet du Réseau Eratosthène, je trouve, mais sans référence, la mention d'un stade de 159,5m.
Rappel: longueur du méridien terrestre 40'008 km (équateur: 40075 km).
Soit une erreur de 3.01 % attribuable en partie au fait que Syène et Alexandrie
ne sont pas exactement sur le même méridien, à l'erreur sur la mesure de
l'angle : 7°12' au lieu de et à la distance de Syène à Alexandrie, dont il
serait surprenant qu'elle soit exactement de 5000 stades tout ronds.
Quelques remarques :
A propos de Posidonios
Posidonios de Rhodes (135-50) mesura la circonférence de la Terre, comme le fit Ératosthène (275-194). Celui-là trouva une
valeur nettement inférieure. D'autres mesures furent par la suite effectuées
par d'autres personnes ; cependant, elles étaient la plupart du temps considérablement
sous-estimées, à l'image de celle de 30 000 kilomètres environ de Ptolémée
au second siècle après Jésus-Christ dans sa Syntaxe mathématique (ou Almageste ).
D'ailleurs, il paraît que cette sous-estimation de 10 000 kilomètres permit
le voyage de Christophe Colomb en 1492, du moment où il ne serait pas parti
s'il avait dû parcourir tant de distance pour rejoindre l'Asie. Néanmoins,
nous n'aurions pas découvert l'Amérique...
Syène
Syène est l'actuel Assouan.
Explication de la nécessité du parallélisme entre les rayons envoyés de divers points du Soleil vers la Terre.
Les rayons sont supposés entre eux parallèles, ce qui n'est pas du tout gênant
en considération de la très grande distance entre le Soleil et la Terre.
En outre, le fait qu'ils soient parallèles permet une comparaison directe
à partir des mesures faites des ombres portées par les objets. La variation
des longueurs des ombres à différents points du globe est alors uniquement
due à la rotondité de la Terre. Par ailleurs, si les rayons ne suivaient
pas une direction parallèle au
voisinage de la Terre, il faudrait des calculs supplémentaires pour déterminer
leur direction. C'est pourquoi Ératosthène prend soin de préciser ce fait
pour étayer sa démonstration.
Lorsque des droites se coupent très loin, elles sont quasiment parallèles.
C'est ainsi qu'un maçon construit les arètes d'une maison avec un fil a plomb.....qui
en vérité donne deux droites sécantes au centre de la Terre!
Enfin, La distance Alexandrie - Syène est de 900 kms environ, ce qui est
négligeable par rapport aux 150 millions de kms entre la Terre est le Soleil.
Erathostène expliqué par le réseau Eratosthène...
http://www.vialattea.net/eratostene/cosmimetria/eratosthene.html
Un commentaire du Monde
« Deux hypothèses s'offraient au savant. Soit la Terre était plate et le
Soleil suffisamment proche pour que ses rayons divergent et provoquent la
différence constatée. Soit notre étoile était très éloignée - dans ce cas,
ses rayons arrivaient parallèles - et seule la rotondité de notre planète
pouvait expliquer les faits. Eratosthène opta pour cette seconde supposition,
car les Grecs soupçonnaient déjà une courbure de la surface terrestre. Ayant
mesuré, à Alexandrie, l'angle que faisaient les rayons solaires avec la verticale,
il n'avait plus besoin, pour calculer la grosseur de notre planète, que de
connaître la distance Alexandrie-Syène, les deux villes étant peu ou prou
sur le même méridien. Cette mesure indispensable lui fut donnée par les caravanes
cheminant le long du Nil entre les deux cités. »
http://www.lemonde.fr/article/0,5987,3244--278486-,00.html
