Retour au sommaire

1. Exposé du problème
2. Quelques données
3. Le cas Pluton
4. Calcul des aspects
5. Etoiles fixes
6. Domitude et heure planétaire
7. Quelques chiffres pour prouver que tout ceci n’est pas pure spéculation de virginien !
8. Angularité
9. Transits
10. Règles pratiques
11. Conclusion
12. Annexe

I Exposé du problème

Cet article a pour but d’attirer l’attention sur les problèmes techniques posés par l’utilisation des latitudes en astrologie.
Prenons un exemple concret pour illustrer notre propos : le ciel de Paris du vendredi 27 Août 1999 à 17:45 TU :

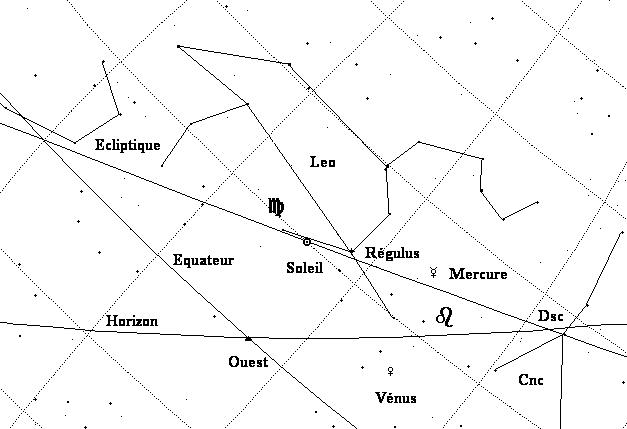
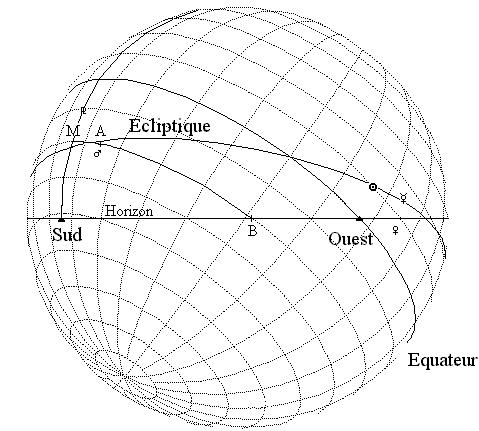
Ce schéma représente une partie de la voûte céleste (2) tel que le verrait un observateur tourné vers l’occident. Relevons quelques points intéressants :
- le Soleil dans le signe de la Vierge, proche de l’étoile Régulus (constellation du Lion)
- Mercure dans le signe du Lion (coucher à 18:27 TU)
- Vénus, elle aussi en Lion, couchée depuis un quart d’heure et par conséquent invisible
- une distance entre Vénus et Mercure comparable à celle qui sépare le Soleil de Mercure.
Sur ces données astronomiques, un astrologue, n’ayant pas oublié que sa pratique est avant tout basée sur l’observation du ciel, notera que le Soleil et Mercure se situent en maison VII et que Vénus invisible sous l’horizon, donc en maison VI, est caractérisée par un forte angularité. De plus notre astrologue ne verra de conjonction qu’entre le Soleil et l’étoile Régulus.
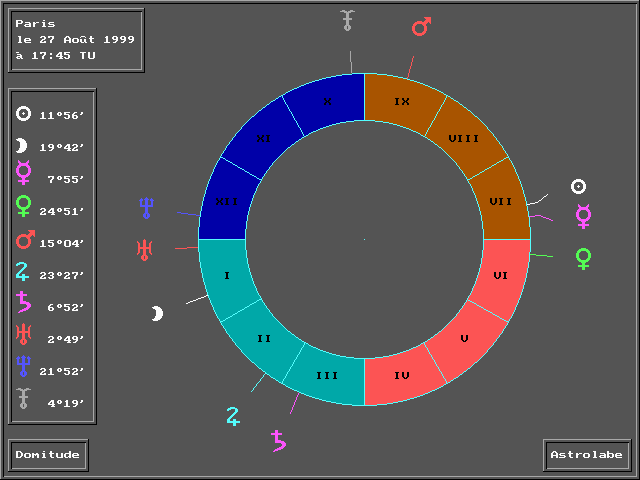
Jetons maintenant un œil sur ce même ciel, tel qu’il est classiquement (3) représenté en astrologie :

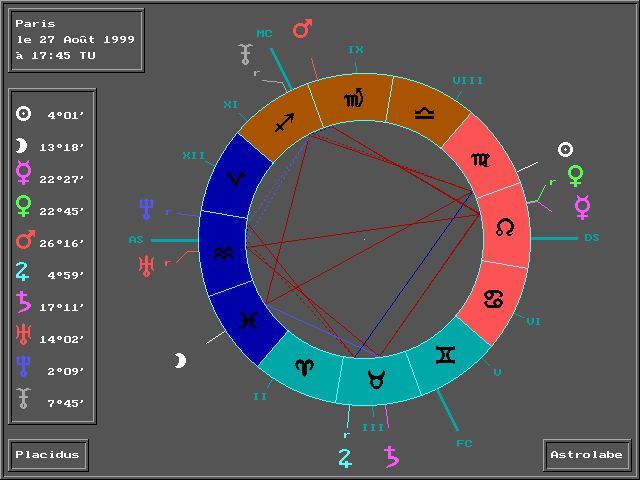
Le malaise est flagrant : Vénus et Mercure apparaissent en conjonction très serrée, et comble de malchance (?), Vénus, qui nous semble ici plus élevée que Mercure, se retrouve en maison VII et perd son statut de planète angulaire !
Et il ne s’agit pas là d’une erreur de calcul mais bien d’un défaut inhérent à la méthode de représentation du ciel natal, qui ne tient compte que de la longitude écliptique des astres et non de la latitude.
Relevons sur des éphémérides (4) les coordonnées écliptiques de nos trois planètes :

Soleil : l = 4° 01’ Vierge, b = 0°
Mercure : l = 22° 27’ Lion, b = 1° 26’ Nord
Vénus : l = 22° 45’ Lion, b = 8° 19’ Sud

Si Vénus et Mercure sont bien à la même longitude, les latitudes sont par contre très différentes. Pour représenter le thème natal nous projetons ces positions sur le cercle écliptique : ceci entraîne une perte de l’information contenue dans la latitude et par conséquent une perte de sens. Ce cas d’école nous montre que le dessin du ciel natal sur une simple feuille de papier n’est pas une chose aussi simple qu’il n’y parait au premier abord. Ne pas tenir compte des latitudes dans l’érection du thème c’est prétendre, dans notre exemple, que Vénus est en maison VII tout en étant sous l’horizon !
Faut-il pour autant abandonner ce type de représentation qui a malgré tout fait ses preuves au cours de ce siècle ? Non, l’important est d’avoir conscience des limites techniques d’un mode de représentation qui donne la préférence au zodiaque plutôt qu’aux maisons (5).

II Quelques données

Ce petit tableau (6) résume la situation en matière d’écarts de latitude :
 

Trois groupes se distinguent : Vénus et Pluton avec une forte amplitude, la Lune, Mars et Mercure, aux variations d’environ 5°, et enfin Jupiter, Saturne, Uranus et Neptune qui restent toujours près de l’écliptique et dont les latitudes peuvent être négligées dans la pratique courante.

III Le cas Pluton

Cette curieuse planète à l’orbite très inclinée pose question avec ces maxima de plus de 17°. Observons la lente évolution de sa latitude au cours du temps :

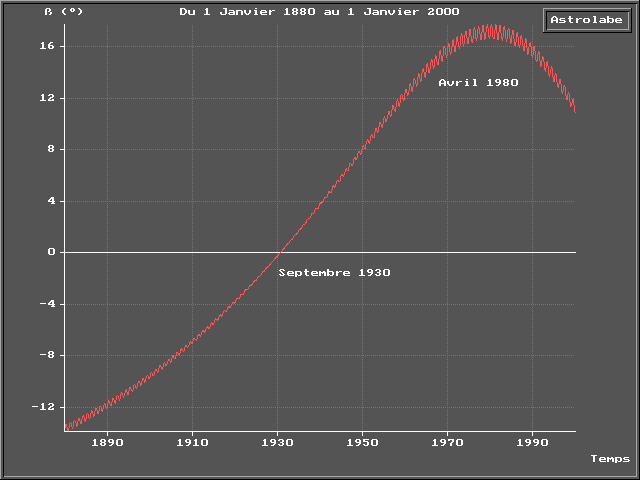
L’on voit sur ce graphique (7) son importance autour des années 1980, avec un maximum en avril 1980 et un minimum en septembre 1930 (année de sa découverte).
Cette courbe, qui vaut toutes les démonstrations, nous montre que toute conjonction « visuelle » avec Pluton est astronomiquement impossible pendant toute une partie de son cycle (aux orbes de conjonction près).
Peut-être appartient-il aux générations d’astrologues nés dans les années 50-80 de se pencher sur ce fait s’il est vrai que l’on ne cherche à résoudre que les problèmes que l’on porte en soi-même. Que l’on puisse négliger les latitudes pour les autres planètes, passe encore, mais avec Pluton, non !
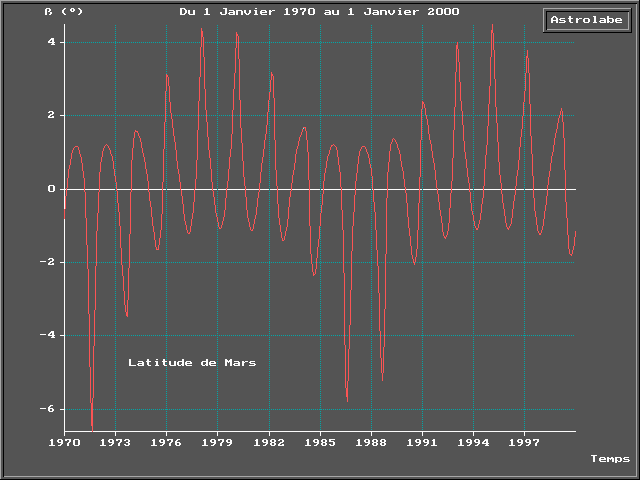
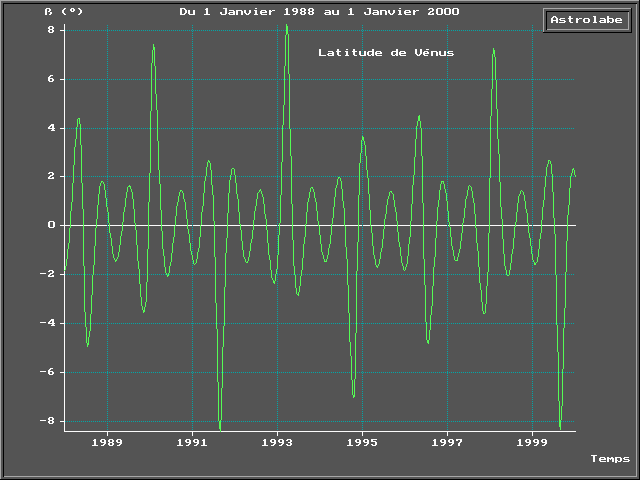
Nous donnons en annexe, à titre indicatif, l’évolution de la latitude de Mars et de Vénus dans les dernières décennies du siècle, et ce, pour montrer que les pics de latitude sont loin d’être des événements rarissimes.

IV Calcul des aspects

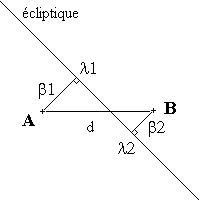
Comment rendre compte de la réalité astronomique dans le calcul des aspects ? Nous proposons une méthode naturelle prenant en compte à la fois longitude et latitude. Son principe est celui de l’arbalestrille, instrument destiné à effectuer des mesures angulaires (cf. l'image au début de ce document). Un observateur terrestre disposant d’un immense compas pose chacune des pointes sur les deux planètes et note simplement l’angle que font entre eux les deux bras. L’astronomie appelle cet angle séparation angulaire des deux astres. Si ceux-ci ont pour coordonnées écliptiques (l1, b1) et (l2, b2), la séparation angulaire d sera donnée par la formule (8) suivante :

formule se substituant à l’habituel l1 - l2, qui en est le cas particulier pour des latitudes nulles (b1 = b2 = 0°).

Ceci s’applique aussi bien aux conjonctions qu’à tous les autre aspects (le calcul habituel des orbes restant inchangé).
L’erreur actuelle du calcul d’aspect est de mesurer des angles entre des points qui n’existent que pour le mathématicien, à savoir les projections de ceux-ci sur l’écliptique.
 

Dans notre exemple d’introduction nous trouvons les valeurs suivantes :

Soleil-Mercure : d = 11° 39’ au lieu de 11° 33’
Soleil-Vénus : d = 13° 58’ au lieu de 11° 15’
Vénus-Mercure : d = 9° 45’ au lieu de 0° 18’ !

La formule de la séparation angulaire tend à se rapprocher de la simple différence des longitudes pour les petites latitudes comme on le voit sur l’exemple. Elle ne présente donc de l’intérêt que lorsque celles-ci sont importantes et agit en quelque sorte comme un filtre éliminant les pseudo-aspects.
Quoique le calcul soit plus complexe, elle recouvre une réalité plus intuitive en rendant compte de ce que perçoit le simple observateur du ciel : l’angle qui sépare deux points lumineux indépendamment de tout référentiel imaginaire.
Elle permet d’apprécier au mieux la valeur astrologique d’un aspect, ceux-ci étant mesurés sur la sphère céleste et non sur l’écliptique (le cercle des aspects est centré sur l’observateur et passe par les deux astres).

V Etoiles fixes

Il va sans dire que cette méthode s’applique à tout objet céleste et en particulier aux étoiles fixes, celles-ci étant caractérisées par des positions quelconques sur la voûte étoilée, les conjonctions ne pouvant réellement avoir lieux que pour les étoiles situées dans l’étroite bande zodiacale (8°½ de part et d’autre de l’écliptique ou 17° si l’on tient compte de Pluton).

L’étoile Régulus de notre exemple nous donne :
Soleil-Régulus : 4° 13’
Mercure-Régulus : 7° 26’
Vénus-Régulus : 11° 16’

VI Domitude et heure planétaire

Avec la technique décrite plus haut nous n’avons résolu que la moitié du problème posé par les latitudes, l’autre concernant la position en maison (9). D’une façon générale les positions calculées des maisons ne valent que pour les astres situés sur l’écliptique (comme le Soleil), dès que ceux-ci s’en écartent, la position en maison à tendance à être faussée, faiblement faussée pour les petites latitudes, franchement fantaisiste pour les grandes latitudes (comme le Pluton des années 80). Le concept de domitude peut nous aider à résoudre ce problème. Observons Mars sur notre sphère céleste. Celui-ci va décrire, dans son mouvement diurne, un arc de cercle parallèle à l’équateur, partant de l’horizon Sud-Est (non visible sur notre schéma), passant au méridien (point M) et se couchant en un point situé au Sud-Ouest (point B) : c’est ce que l’on appelle son arc diurne (10). La « longueur » de celui-ci dépend de la déclinaison de l’astre et de la latitude du lieu.

La valeur du semi-arc diurne (angle entre le point M et le point B) est donné par la formule :

où D est la déclinaison de l’astre et Phi la latitude géographique du lieu.
Ce semi-arc ne vaut 6 heures que pour un astre situé sur l’équateur. Dans ce cas l’arc diurne est égal à l’arc nocturne et les « jours » de l’astre sont égaux à ses « nuits ». La notion de domitude est très proche de celle d’heure planétaire (11) : découpons ce semi-arc en trois parties égales entre elles, nous obtenons trois maisons diurnes iso-horaires (c’est-à-dire parcourues par l’astre en des temps égaux). La domitude exprime la proportion entre l’angle horaire (12) (réduit à son cadran, c’est à dire à une valeur inférieure à 90°) et la valeur du semi-arc sur lequel se trouve cet astre. Inutile donc de dire que la domitude ne peut être calculée que pour les astres qui se lèvent. Le tableau suivant donne la formule de la domitude dans les quatre cas de figure possibles (13) :
 

Elle est comptée dans le sens direct à partir du levant, et ceci pour suivre l’ordre traditionnel des maisons (14), et c’est là qu’elle se sépare des heures planétaires qui elles, sont comptées à partir du levant dans le sens diurne (le sens des aiguilles d’une montre !). L’heure temporelle est reliée à la domitude par la formule :

C’est par abus de langage que l’on note la domitude en degrés, car celle-ci ne représente réellement un angle mesurable que pour un astre situé sur l’équateur, dans ce cas l’arc diurne vaut 180° (12 heures), et la domitude correspond alors à une sorte d’angle horaire qui serait mesuré dans le sens direct à compté du point Est. Dans tous les autres cas la domitude ne peut être assimilable à un angle, ses valeurs vont de 0 à 180 pour les maisons nocturnes et de 180 à 360 pour les maisons diurnes, la culmination étant repérée par la valeur 270, chaque maison valant 30.

Mars de notre exemple (déclinaison 21°02’ Sud et angle horaire 42m 25s) nous donne une domitude de 255 (à mi-chemin dans la maison IX) et donc une heure planétaire de 7h.
De même pour Vénus à 24.8 de la maison VI, Mercure à 7.9 de la VII et le Soleil à 11.9 de la VII (figure ci-dessus).

VII Quelques chiffres pour prouver que tout ceci n’est pas pure spéculation de virginien !

Je me suis livré à une petite statistique pour savoir dans quelle proportion les domifications de planètes étaient erronées.
J'ai monté 10 000 thèmes (naissances sur Paris) répartis aléatoirement en date et en heure entre 1800 et 2000.
Et j'ai comparé la maison obtenue avec une domification qui ne tient pas compte de la latitude avec la maison obtenue par celle qui en tient compte. Voici l'intéressant résultat de cette recherche :
 

Quelques commentaires sur cet éloquent tableau :
- le quart des positions de Pluton en maison sont fausses ! Ce qui n’a rien d’étonnant vu l’importante latitude de la planète.
- plus surprenant, presque 8 % des domifications de la Lune le sont également !
- l’on voit sur ce tableau que si les pics de latitude de Vénus et Mercure sont importants, leurs relatives raretés rends l’erreur statistiquement moins importante.
Je laisse méditer le lecteur sur ces chiffres...

VIII Angularité

Qu’est-ce que l’angularité d’une planète ? Deux définitions sont possibles ; la première, implicite dans la pratique astrologique courante, est la suivante : une planète est dite angulaire lorsque la longitude de celle-ci est proche d’un des quatre points clés du thème (ascendant, descendant, milieu du ciel et fond du ciel). Dans ce cas l’appréciation se fait à la simple vue du thème.
La première figure montre bien l’insuffisance d’une telle définition : Vénus très éloignée du descendant n’en est pas moins à un quart d’heure de son coucher.
Aussi doit-on introduire une autre définition (15) : une planète sera dite angulaire si elle est proche de son lever, de son coucher, de sa culmination ou de son passage au fond du ciel. La domitude de la planète sera alors toute indiquée pour mesurer la force de cette angularité. La plus ou moins grande proximité des valeurs 0 (AS), 90 (FC), 180 (DS) et 270 (MC) mesurera l’angularité de la planète.
Notons que cette formulation à partir de la domitude est très pratique lorsque l’on veut rechercher par le calcul la dominante planétaire, celle-ci devant prendre en compte, entre autres facteurs, l’angularité des planètes (dans l’indice de Jacques Berthon par exemple).

IX Transits

L’introduction des latitudes raffine quelque peu la pratique des transits, si nous postulons qu’un transit est d’autant plus efficient que la séparation angulaire entre la planète transitée et l’astre appliquant est plus petite (16). Une telle idée est bien entendue à soumettre à l’épreuve de la pratique.
Montrons sur un exemple ce que nous entendons par là ; prenons un thème connu de tous, celui du Président Jacques Chirac (Paris, 29 Novembre 1932 à 12:00) et étudions le transit de Mars sur son Jupiter radical entre le 1 Novembre 1996 et le 1 Juillet 1997. Ce transit de longue durée est remarquable par la boucle céleste qu’effectue Mars dans le ciel pendant cette période.

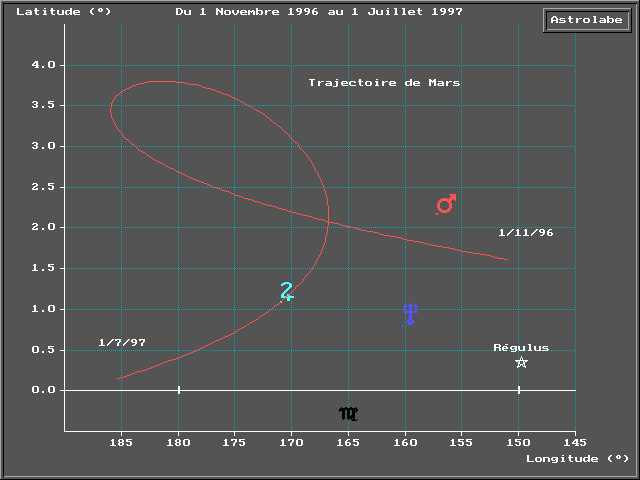
Ce premier graphique représente la trajectoire de Mars en coordonnées écliptiques pendant ces 8 mois. Sont aussi représentées les planètes du thème présentes dans le signe de la Vierge (Mars, Neptune et Jupiter). La latitude nous aide à percevoir plus finement les principales phases de ce transit martien sur Jupiter : l’application, la première station, la rétrogradation, la deuxième station et enfin le dernier passage de Mars. Et nous voyons nettement la différence entre le premier passage à 1° d’orbe, le deuxième à 2° et le dernier, pratiquement exact. De nombreux cas de figure sont envisageables en pratique, planète encerclée par une boucle, trajectoire lointaine d’une planète, etc.
Une autre façon de représenter ce transit virginien est la suivante : mesurons à tout instant la séparation angulaire entre Mars et le Jupiter radical, nous obtenons un nouvelle courbe. Les dates clés du transit y apparaissent plus clairement encore. Les trois minimum de la courbe correspondent aux minimum de distance entre Mars et Jupiter (la non utilisation de la latitude ferait apparaître trois creux à 0°). Le dernier passage, autour du 25 Mai, y est visiblement le plus intense (à suivre avec intérêt...) (17).

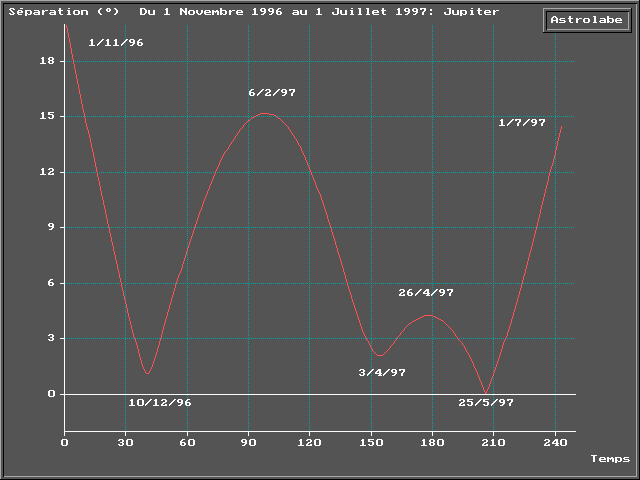
Ce type de représentation a aussi l’intérêt de permettre l’appréciation des orbes de transit en nombre de jours (ce qui est autrement plus parlant qu’un angle).

X Règles pratiques

Essayons d’énoncer quelques règles pratiques à l’usage de ceux qui érigent le thème « à la main ».
Pour la Lune, un bon point de repère pour sa latitude est sa position par rapport au nœuds nord et sud, un angle de 90° indiquant une latitude d’environ 5°, et la proximité de ceux-ci une latitude négligeable. Les nœuds de Vénus, Mars et Mercure n’étant pas indiqués dans les éphémérides courantes, nous n’en dirons donc rien (jetez néanmoins un œil sur les pics des deux courbes données en annexe).
Pour Pluton la latitude peut être négligée dans les années 1910 à 1950, le passage au nœud nord s’effectuant en 1930 ; pour les années suivantes, méfiance, la position en maison tend à être faussée, de même pour le début de ce siècle. Remarquons que l’erreur commise est plus grande à proximité de l’horizon qu’au méridien (elle dépend aussi de l’inclinaison locale de l’écliptique).

XI Conclusion

Nous ne prétendons pas introduire des concepts nouveaux mais simplement faire appels aux fondements astronomiques de l’astrologie en insistant sur les trois grands problèmes posés par les latitudes : les conjonctions, la position des astres en maison et son corollaire, l’angularité. Les phénomènes décrits sont loin d’être rares aussi serait-il bon d’envisager sérieusement la prise en compte de la latitude dans l’érection du thème de naissance ; il faut le dire, nombre d’interprétations, parfois même brillantes, sont basées sur des données fausses. Malgré les quelques règles pratiques énoncées, les solutions décrites plus haut demandent bien entendu une mise en œuvre informatique (18), personne ne songeant plus aujourd’hui à faire ces calculs à la main.
N’ayant guère été abordée jusqu’ici (19), la question des latitudes reste ouverte à l’investigation...
 

Remerciements aux quelques personnes qui ont bien voulu assurer une première lecture de ce texte : Max Duval, Didier Geslain, S.V.H., Etienne Lenoble, Yves Lenoble & Maryse Varaillac.

Notes :

1) Tetrabiblos, p.62, Editions Vernal / Philippe Lebaud. Retour

2) Dans une fenêtre de 59° sur 40°. Retour

3) Du moins en France depuis Paul Choisnard. Retour

4) Les éphémérides du commerce ont hélas pris la curieuse habitude de donner longitude écliptique et déclinaison équatoriale sans indication de la latitude, interdisant par là les calculs décrit plus bas. Retour

5) Signalons néanmoins la belle tentative de Jean Hiéroz, dans son livre sur Morin, où cet auteur propose l’utilisation de l’Astrolabe comme moyen de « représentation mathématique exacte » du thème ; ou encore le thème de domitude d’Yves Lenoble, complétant la représentation de Choisnard. Retour

6) Statistiques effectuées de l’an 1500 à l’an 2000 (excepté pour Pluton). Retour

7) Les oscillations sont dues au cycle annuel de la Terre autour du Soleil. Retour

8) Cette formule s’applique également en utilisant l’ascension droite et la déclinaison des astres. Retour

9) Nous nous situons dans cette note uniquement dans le cadre de la domification horoplanétaire (dite de Placidus), il existe en effet d’autres calculs de la domitude (Campanus). Retour

10) Arc nocturne dans le parcours nocturne de l’astre. Retour

11) « Les Astrologues ont été amenés à prendre en considération une autre division du temps : les heures planétaires dites encore heures inégales. Cette division consiste à partager en douze parties égales (heures diurnes) le temps durant lequel un astre se trouve au-dessus de l’horizon, et en douze autres parties (heures nocturnes) le temps de son séjour au-dessous. » Jean Hiéroz, L’Astrologie selon Morin de Villefranche, Omnium Litteraire. Retour

12) L’astronomie mesure l’angle MA, appelé angle horaire H, compté positivement dans le sens diurne à partir du demi-méridien Sud (rappelons que H = TS - Alpha). Retour

13) Cf. Mémoire de DESS d’Yves Lenoble d’où nous tirons la formule (en changeant la convention d’origine des angles horaires). Retour

14) Pendant longtemps nous nous sommes demandé pourquoi les astrologues numérotaient les maisons dans le sens inverse du mouvement diurne, alors que celles-ci sont justement liées à ce mouvement. Jusqu’au jour où un cadran solaire mural nous tomba sous les yeux : les heures y sont, de part le principe même de cet instrument, numérotées dans le sens inverse des aiguilles d’une montre, et l’on sait que le moyen le plus usuel de mesurer le temps, au temps où l’Astrologie vit le jour, était celui-là (avec la clepsydre), alors peut-être est-ce là l’origine de ce renversement ? Retour

15) Définition qui ne s’applique pas aux régions circumpolaires. Retour

16) Max Duval note à juste titre : « On peut toutefois penser qu’un transit par conjonction notamment possède toute chance de se montrer d’autant plus efficient que la latitude de la planète transitante est d’autant plus voisine de la position natale transitée. », La domification et les transits, p. 75, Editions Traditionnelles. Retour

17) L’objet de cet article n’est pas d’interpréter ce transit, notons simplement pour mémoire que le Jeudi 11 Décembre 1996, M. Chirac fit une conférence de presse TV (Mars / Jupiter : extériorisation de l’action).
J'écrivais ces lignes en janvier 97, la suite des événements a montré l'intensité de ce transit (dissolution de l'assemblée et élections législatives du 25 mai avec les résultats que l'on sait). Retour

18) Notre logiciel « freeware » est à la disposition du lecteur intéressé par ce sujet à l’adresse internet suivante : http://perso.cybercable.fr/hermes/. Retour

19) Les articles d’André Barbault sur « les occultations en astrologie mondiale » (L’Astrologue n° 20) et « les nœuds en astrologie individuelle et mondiale » (n° 23), contiennent des réflexions sur le sujet. Retour

XII Annexe

© Jean-Christophe Vitu, 1997-1998

Retour au sommaire