f(x) = ............ sur [... ; ....]
f(x) = ............ sur [... ; ....]
f(x) = ............ sur [... ; ....]
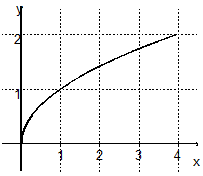
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Activité 1.
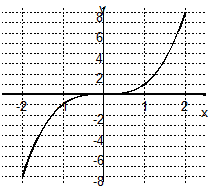
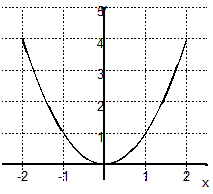
Proposer une formule, un intervalle d'étude et compléter le tableau de variation pour chacune des fonctions tracées ci-dessous.
|
f(x) = ............ sur [... ; ....] |
f(x) = ............ sur [... ; ....] |
f(x) = ............ sur [... ; ....] |
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
Parmi les trois fonctions décrites ci-dessus dire laquelle est paire, laquelle est impaire et laquelle n'est ni paire ni impaire.
Activité 2.
|
Etude de la fonction f(x) = 2x2 sur [-2 ;2] |
Etude de la fonction f(x) = 0,5x2 sur [-2 ; 2] |
||||||||||||||||||||||||
|
Tableau de valeurs :
|
Tableau de valeurs :
|
||||||||||||||||||||||||
|
Représentation graphique :
|
Représentation graphique :
|
||||||||||||||||||||||||
|
Tableau de variation :
|
Tableau de variation :
|
||||||||||||||||||||||||
|
Parité : |
Parité : |
|
Conclusion :
|
Exercice.
Relier les formules aux graphiques et aux tableaux de variation.
|
f(x) = 4x2 sur [-2 ; 2] |
f(x) = 0,8x2 sur [-2 ; 2] |
f(x) =
|
||||||||||||||||||||||||||||||||||||
|
• |
• |
• |
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
• |
• |
• |
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
• |
• |
• |
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
• |
• |
• |
||||||||||||||||||||||||||||||||||||
|
|
|
|---|
Activité 3.
À l'aide du logiciel : Grapheur Compléter les tableaux de variation et écrire un petit commentaire.
|
fonction |
Tableau de variation |
commentaire |
||||
|
f(x) = x2 sur [-3 ; 3] |
|
|
||||
|
f(x) = 3x2 sur [-3 ; 3] |
|
|
||||
|
f(x) = -3x2 sur [-3 ; 3] |
|
|
||||
|
f(x) = 0,25x2 sur [-3 ; 3] |
|
|
||||
|
f(x) = -0,25x2 sur [-3 ; 3] |
|
|
|
Conclusion :
|
Activité 4.
À l'aide du logiciel : Grapheur
Tracer sur [-3 ; 3] les fonctions suivantes, compléter les tableaux de variation et écrire un petit commentaire.
|
fonction |
Tableau de variation |
commentaire |
||||
|
f(x) = 2x2 sur [-3 ; 3] |
|
|
||||
|
f(x) = 2x2 + 3 sur [-3 ; 3] |
|
|
||||
|
f(x) = 2x2 – 3 sur [-3 ; 3] |
|
|
|
Conclusion :
|
Exercice 1.
Pour les fonctions décrites ci-dessous, sans les tracer, compléter leurs tableaux de variation après avoir calculer quelques valeurs.
|
Fonction |
valeurs |
Tableau de variation |
||||
|
f(x) = 2x2 – 3 sur [-2 ; 2] |
f(-2) =
f(0) =
f(2) =
|
|
||||
|
f(x) = -0,7 x2 + 2 sur [-2 ; 2] |
f(-2) =
f(0) =
f(2) =
|
|
||||
|
f(x) = |
f(-2) =
f(0) =
f(2) =
|
|
Exercice 2.
Associer chaque expression à sa représentation graphique.
|
|
|
|
|
• |
• |
• |
|
|
|
|
|
• |
• |
• |
|
f(x) =
|
f(x) = 2x2 – 2 sur [-2 ; 2] |
f(x) = -2x2 + 6 sur [-2 ; 2] |
CH Page