Международная школа творчества Профессора
Григория В. Томского: Математические проблемы ЖИПТО
Математические проблемы ЖИПТО
Для математических моделей ЖИПТО способные школьники, их учителя и все любители математики могут проанализировать следующие две основные проблемы.
Проблема "преследователя". Найти стратегии (способы действий) "преследователя", гарантирующие ему как можно лучший результат в игре.
Проблема "убегающих". Найти стратегии (способы действий) "убегающих", гарантирующие им как можно лучший результат в игре.
В математических моделях ЖИПТО диаметр позиции "убегающих" равен числу
D, причем обычно D = 2. Можно рассматривать также игры с
D < 2. В пределе, устремляя D к нулю, мы получаем идеальную математическую модель ЖИПТО. В этой модели позиции "преследователя" и "убегающих" являются геометрическими точками, а траектории являются линиями. Такая модель часто более удобна для математического исследования, полученные полезны для анализа версий ЖИПТО с достаточно маленькими диаметрами фишек.
Обозначим через P(t) позицию "преследователя"
(P) и через F(t) позицию "убегающиго"
(F) в момент времени t. Партия игры начинается в момент времени
t = 0. Моменты раздумывания ходов не засчитываются.
Линия, состоящая из точек P(t) называется траекторией
P. Траекторией F является линия, состоящая из точек F(t). При этом должны выполняться условия
P(s) P(t) < a(t - s), F(s) F(t) < b(t - s) для t > s, где
a - максимальная скорость P и et b - максимальная скорость
F, причем обычно a = 2, b = 1. Заметим, что в идеальной математической модели ЖИПТО, "преследователь" и "убегающие" могут менять направление своего движения в любой момент времени.
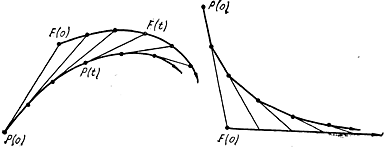
Изучение простых случаев дает способным ученикам первые опыты математического исследования.
Можно, например, уменьшить число "убегающих", рассматривать игры, в которых "убегающие могут менять направление своего движения только два раза или могут двигаться только по нескольким направлениям.
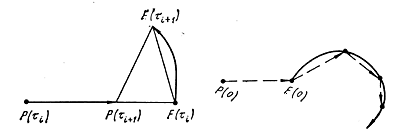
Более глубокий анализ может привести к новым математическим результатам.
<<<Назад