Nous voyons ici le profil d’une aile type avec sa profondeur, son épaisseur et la surface de contact du solide avec le milieu extérieur.

Les deux coefficients Cx et Cz sont des caractéristiques d’une aile, qui peuvent varier selon les conditions du milieu ou bien même avec l’usure de l’aile dans le temps. On peut ainsi dire que ces coefficients illustrent les qualités aérodynamiques d’un certain volume solide dans un environnement donné. Le coefficient Cx de l’aile est un coefficient qui est fonction de la traînée. Il indique l’importance du « défaut résiduel » qui entraîne des frottements avec l’air.

         Le coefficient Cz d’une aile est quant à lui la capacité de ce volume à transformer en portance les nombreuses forces exercées sur lui par les courants d’air autour de lui. Ainsi, ce coefficient illustre la capacité d’un avion à se maintenir en l’air.

         Néanmoins, tout au long du déplacement du planeur, ces coefficients varient selon les conditions environnementales constamment changeantes.

         Ensuite, l’aile doit posséder certaines caractéristiques optimales pour diminuer sa prise à l’air qui pourrait la retarder:

• elle élimine les écoulements marginaux car ils forment des tourbillons à  l’arrière de l’aile et ces tourbillons risquent de déstabiliser l’aile en créant des oscillations.
• elle doit posséder une résultante aérodynamique positive c'est-à-dire qu’elle doit pouvoir être aspirée sur sa face supérieure et poussée sur sa face intérieure.

Ainsi, les écoulements, qui désignent le déplacement de l’air par rapport à l’aile,  autour d’une aile ne doivent pas gêner le comportement d’un planeur en vol. En effet ils augmentent significativement la traînée de l’appareil. Trois types d’écoulements sont à identifier :

1. l’écoulement laminaire : les filets d’air (suite de particules d’air suivant une même trajectoire) ont des trajectoires rectilignes et parallèles entre eux. On rencontre ce type d’écoulement dans un milieu où l’air ne rencontre aucun obstacle.

2. l’écoulement turbulent : les filets se déplacent par ondulations dans le même sens. Cet écoulement est caractéristique d’une bonne aile car il ne perturbe pas la trajectoire du planeur.

3. l’écoulement tourbillonnaire : les filets d’air forment des tourbillons sur les extrémités de l’aile d’où la création de vortex parasites que nous allons étudier.

Pour diminuer cette traînée, il faut réduire l’influence des tourbillons et donc allonger les ailes dans leur longueur.

L’aile obtenue est dite en creux et possède un bord d’attaque épais tandis que le bord de fuite est plus fin tout en gardant une épaisseur suffisante pour ne pas être trop fragile.

         Enfin écoulement de l’air est moins turbulent sur des surfaces courbes car les filets d’air «  collent » mieux sur ce type de surface. Prenons pour exemple un verre d’eau : si vous le couchez horizontalement dans un évier et que vous laissez couler un mince filet d’eau sur sa tranche, vous vous apercevrez que l’eau glisse sur sa surface extérieure et colle au verre. C’est la même chose qui se produit avec l’air et l’aile : l’air « colle » à la surface de l’aile.

         Ainsi l’air contourne facilement la plaque de l’aile même si l’existence de zones tourbillonnaires n’est pas à exclure totalement.

         Pour comprendre cela, il faut tout d’abord savoir que la vitesse parcourue par un flux d’air n’est pas la même à l’extrados et à l’intrados d’une aile selon le principe de Bernoulli. Je m’explique : lorsque l’on regarde une aile de planeur en coupe, on s’aperçoit que sa face supérieure appelée extrados est plus convexe que la face inférieure de l’aile qui, elle, est droite. On en conclut que la distance parcourue à l’extrados est plus grande que celle parcourue à l’intrados.

Or, on connaît la formule :        

Mais Bernoulli a démontré, avec son « principe des temps de transition égaux », que les masses d’air qui traversent un solide avec une certaine vitesse se séparent en deux au bord d’attaque de l’aile et que les deux parties de la masse d’air initiale se rejoignent ensuite au bord de fuite. Voici une application qui pourra vous aider à comprendre :

Schéma représentant une aile traversant un flux d’air de gauche à droite: les deux parties de ce flux se séparent et se rejoignent au bord de fuite.

On sait que la distance parcourue, pour un même intervalle de temps, est supérieure à l’extrados qu’à l’intrados. On en conclut que la vitesse augmente à l’extrados par rapport à l’intrados.

          Le profil de l’aile qui en résulte est une aile constituée d’une plaque courbe. Et c’est ici qu’intervient la notion de distance sur le profil de l’aile selon Bernoulli. La vitesse augmente donc à l’extrados et diminue à l’intrados pour créer une dépression au-dessus de l’aile et une surpression sous l’aile.

         En effet, vitesse et pression varient inversement dans l’écoulement d’un fluide c’est à dire que si la vitesse augmente alors la pression diminue et si la vitesse diminue alors la pression augmente d’après Bernoulli.

On arrive ainsi à une équation définie par Bernoulli qui lie la pression et la vitesse par une constante :

Donc une aile constituée d’une plaque courbe bombée sur l’extrados conduit à une accélération de l’air au dessus de l’aile tandis que la vitesse de l’air en dessous diminue. D’où une diminution de la pression sur l’extrados et une augmentation sous l’intrados.

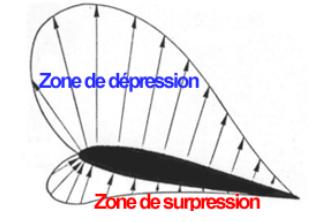
Une aile créant deux zones de pressions différentes à l’extrados et à l’intrados.

C’est cette différence de pression qui est ici importante : elle va induire une double poussée ascendante visant à maintenir l’avion en vol. Du fait de la dépression au-dessus de l’aile, le milieu va  « tirer » l’extrados de bas en haut pour annuler la dépression tandis que le milieu sous l’aile va pousser du bas l’intrados pour répartir la surpression.

            D’après le principe de Bernoulli, la portance est bel et bien  une force constituée de cette double poussée (deux forces colinéaires et de même sens). Nous venons de démontrer le fait que l’aile ne prend pas appui sur l’air mais qu’elle crée son propre milieu pour se maintenir en l’air grâce, justement, à son profil.

 

          Enfin, on peut donc calculer la portance et la traînée toutes deux en Newton N d’après Bernoulli:
                          Calcul de la portance : Rz=0.5∙ρ∙V²∙S∙Cz
                          Calcul de la traînée    : Rx=0.5∙ρ∙V²∙S∙Cx

                    Rz et Rx représentent la portance et la traînée (N).
                    ρ est la masse volumique de l’air (kg/m³).

                    V est la vitesse du vent relatif (m/s).
                    S  est la surface de l'aile  (m²).

 

Mais pouvez-vous me faire réellement confiance lorsque je vous dis qu’un seul type d’aile conduit à la génération de la portance ? Est-on vraiment sûr que l’on pourrait faire voler une aile comme je l’ai décrite ? Pour le savoir, il n’y a qu’une seule solution : tester notre hypothèse et c’est ce que nous avons fait très simplement.

Nous avons donc créé une aile plate et une aile courbée et envoyé un flux d’air dessus. Voici les résultats avec l'aile plate et avec l'aile courbée.

Nous pouvons seulement conclure que notre hypothèse est vérifiée. L’aile courbée à l’extrados monte tandis que l’aile droite ne bouge pas.

Image tirée de notre vidéo et présentant les conditions de l’expériences.

       Mais cette expérience nous renseigne sur un autre point qui semble évident mais à ne pas omettre : l’aile et donc le planeur a besoin de posséder une vitesse par rapport au milieu : son vent relatif. Comment le créer ? Comme le planeur n’a pas d’hélice, il doit plonger la tête la première vers le sol et ainsi conserver une vitesse donc une portance si ses ailes sont bonnes.

      Pour conclure cette partie, on peut dire que selon Bernoulli, le profil de l’aile influe sur la sustentation et le déplacement du planeur en l’air.

   
         2)Remise en cause de ce principe :

     Le principe de Bernoulli repose sur le fait que c’est uniquement l’aile qui induit le phénomène de portance. En effet, de par sa forme, plus ou moins convexe à l’extrados et le plus souvent rectiligne à l’intrados, l’aile induit une vitesse de l’air plus grande au-dessus de l’aile qu’en dessous comme nous l’avons démontré. Ceci repose sur le  principe des temps de transitions égaux.

 

       Mais pourquoi donc ce principe serait valide dans notre cas ? Et c’est ici que le principe de Bernoulli rencontre une faille. Un flux d’air qui se sépare au bord d’attaque d’une aile ne se recompose pas au bord de fuite. On remarque dans le dessin suivant que si on introduit un nuage vertical à un instant donné τ et qu’on lui donne un vitesse en direction de l’aile, ce nuage se sépare au bord d’attaque mais que l’air passant sousl’aile est ralenti de telle sorte que le flux passant par l’extrados « sort » plus vite du bord de fuite que lui.

Schéma représentant l’écoulement d’un même flux d’air à l’extrados et à l’intrados d’une aile.

         Peu de personnes ont osé remettre en cause ce principe mais nous pouvons citer Gail Craig qui a essayé de vulgariser une contre hypothèse au principe de Bernoulli dans son ouvrage Stop abusing Bernoulli !  où il démontre par l’absurde que dans le cas d’un avion ce principe est faux.
      
       Néanmoins, l’explication de Bernoulli n’est pas fausse. Elle se base seulement sur des données erronées : on ne peut pas appliquer ici le principe des temps de transition égaux. Pour convaincre les plus pessimistes quant à la validité de cet énoncé, il suffit de prendre un exemple auquel nous aurions appliqué le principe de Bernoulli : si nous voulions générer assez de portance pour un planeur dont la  distance du bord d’attaque au bord de fuite sur l’extrados est supérieure de 3% à celle de l’extrados, nous devrions faire voler ce planeur à environ 600 Km/h. A l’inverse, la longueur de l’extrados d’un planeur se déplaçant à une vitesse moyenne devrait être 50% plus importante que l’intrados. C’est là que le principe des temps de transition égaux se révèle inexact.

Forme d’une aile si l’on ne prenait en compte que le principe de Bernoulli !

Pour conclure cette partie, le principe de Bernoulli expliqué précédemment n’a rien de faux. Il se base seulement sur un théorème erroné. Ainsi, on voit sur le schéma de la page précédente qu’une aile dont le bord d’attaque est orienté vers le haut semble réduire la vitesse de l’air.

            Notre explication aurait donc été incomplète si nous nous étions basés seulement sur le fait que l’air obéit dans ce cas au principe de temps de transition égaux mais il était nécessaire d’expliquer ce théorème de Bernoulli pour clarifier notre raisonnement.