B] Mécanique,
physique
de vol :
Jusqu’ici, nous avons
vu comment un planeur réussissait à se maintenir en
l’air en admettant qu’il
conservait une vitesse constante durant tout son vol. Ce
phénomène de
sustentation est exactement le même qui régit le vol
d’un avion
à réacteur.
Cependant, un avion traditionnel possède, contrairement au
planeur, une source d’énergie
directe : le
carburant, lequel lui permet grâce à ses moteurs de
fournir l’énergie
nécessaire pour justement garder sa vitesse. Mais par
définition un planeur est
un « engin volant non motorisé ».
Dès lors, et c’est ce qui fait
toute sa spécificité, un planeur doit puiser son
énergie
« ailleurs » : un
« ailleurs » pour l’instant
mystérieux voire magique que nous nous proposons
d’expliquer dans cette partie.
III) Origine de cette énergie:
1) Bilan dynamique en
l’air :
Tout d’abord,
faisons un rapide
bilan sur ce qu’advient à un planeur immobile au sol, dans
le référentiel
Terre
supposé galiléen. Il est soumis à deux
force : son poids indissociable de
tout corps et la réaction du sol. Maintenant, plaçons
nous en l’air lors du vol
d’un de ces appareils et regardons ce qui se passe de plus
près dans le
référentiel Air galiléen.
En
réalité, un planeur ne
vole pas, comme un avion, mais il
« plane », ce qui signifie qu’il descend
toujours lentement vers le
sol à un taux fixe. Pour quelle raison ?
Prenons dans un
premier temps le problème à l’envers :
imaginons donc un planeur générant
suffisamment de portance pour voler, que se passerait-il s’il
suivait une
trajectoire horizontale ? Il tomberait tout simplement,
puisqu’il serait,
comme tout corps se déplaçant dans un fluide, victime de
la résistance de l’air
: la traînée, qui le freinerait inévitablement. En
effet, il convient ici de
citer la première loi de Newton ou principe d’inertie: « Dans
un
référentiel galiléen, lorsqu'un solide est
isolé ou pseudo isolé (sa résultante
des forces est nulle), son centre d'inertie G est soit au repos, si G
est
initialement immobile, soit animé d'un mouvement rectiligne
uniforme. ». Selon ce principe,
notre planeur est dit non pseudo isolé dans cette position, et
il ne pourrait que suivre un mouvement rectiligne retarde. En effet, on
peut le déduire de la deuxième loi de Newton car: la
résultante des forces correspondant à la
traînée est colinéaire au vecteur ΔVG et de
sens opposé (elle s'oppose au mouvement).
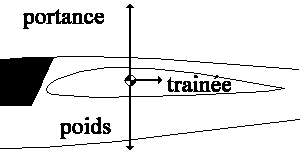
Bilan des forces
s’exerçant sur
un planeur volant horizontalement.
La solution est donc
de perdre de l’altitude. Analysons donc ce
phénomène plus précisément.
Celui-ci se base
aussi selon le principe d’inertie. En effet, il suffit que notre
planeur soit
pseudo isolé pour qu’il conserve sa vitesse ! Comment
faire ? Créer
artificiellement une force compensant la traînée. Dans
notre cas on ne peut pas
changer grand-chose à l’orientation du poids, mais
portance et traînée
dépendent de l’orientation du planeur dans l’espace.
Mais si on incline
légèrement le nez du planeur vers l’avant, on
arrive à créer une résultante
aérodynamique (somme des forces portance et
traînée) compensant exactement le
poids. Concrètement on obtient ceci :
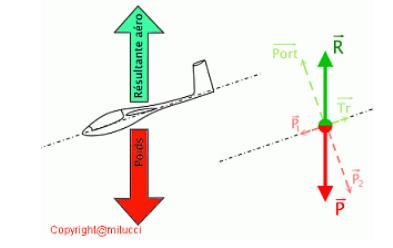
Bilans des forces
s’exerçant sur
un planeur suivant une trajectoire inclinée en l’air.
On remarque très bien
que dans cette position, toutes les forces extérieures
s’appliquant au système
{planeur} se compensent et ce dernier peut donc réussir à
conserver sa vitesse.
Il faut préciser qu’il ne peut pas être au repos
comme le suggère la première
loi de Newton puisque il possède une vitesse initiale, laquelle
a été donnée au
décollage soit par un avion remorqueur, un treuil ou encore un
petit moteur
intégré au planeur et rétractable pour la suite du
vol.
Ainsi, un tel
appareil avance car une composante de son poids
l’entraîne vers l’avant,
ce qui le distingue des avions à réacteur qui, eux, vole
suivant une
trajectoire horizontale, la poussée s’opposant à la
traînée.
2)
Bilan
énergétique :
Cependant, on peut
aussi
expliquer la mécanique « du vol
plané » en s’intéressant plus
précisément aux transferts d’énergies,
c’est-à-dire en réalisant un
bilan énergétique du système {planeur} en
l’air.
En effet, on a
déjà vu qu’une certaine
puissance, était indispensable pour
pouvoir voler. Et c’est ici qu’intervient la notion du travail d’une
force.
Lorsqu’une force s’exerçant sur un système
travaille de façon motrice, celui-ci
gagne de l’énergie ; et lorsque qu’elle
travaille d’une manière
résistante, celui-ci en perd. Ce phénomène
s’applique parfaitement au planeur :
la traînée travaille dans le sens opposé au
mouvement du planeur, on dit
qu’elle « consomme » en quelque sorte de
l’énergie.
Le
planeur, quelque soit sa phase de vol, possède une
réserve d’énergie mécanique
notée Em somme de deux d’énergies
différentes :
- Energie
cinétique de formule Ec=1/2mV²
- Energie potentielle
de pesanteur telle que Ep=mgz
Avec m
la masse du
planeur.
V sa vitesse.
z l’altitude du planeur.
g l’intensité de la
pesanteur.
Ainsi une diminution de
l’énergie
cinétique équivaut à une diminution de la vitesse
du planeur; et une perte
d’énergie potentielle équivaut à une perte
d’altitude.
Si le système
était conservatif, les échanges
entre ces deux énergies seraient infinies et le planeur pourrait
gagner de la
vitesse en perdant de l’altitude et inversement. Mais ceci
est valable
dans le cas où seul le poids travaille. Or les frottements entre
l’air et
l’appareil sont loin d’être négligeables, la
traînée travaille, le système
n’est alors plus conservatif, et son énergie
mécanique totale diminue
inexorablement sans aide extérieure.
=> Dès lors
deux cas se présentent
à nous :
- Si
on décide de fixer l’énergie potentielle, on ne
perd plus
d’altitude. Mais la traînée entre autre va puiser
son énergie là ou elle le
peut c’est-à-dire dans l’énergie
cinétique. Le planeur perd donc de la
vitesse ! Cela n’est donc pas une bonne solution pour voler.
- Mais
si on décide de laisser l’énergie potentielle comme
source
d’énergie ou la traînée pourrait venir puiser
ce dont elle a besoin, on
arriverait à conserver une énergie cinétique
constante. Ceci équivaut à voler
en ligne droite, à vitesse constante tout en perdant de
l’altitude, et rien ne
peut plus s’opposer au planeur jusqu’au sol.
Finalement, on aboutit au fait que pour
voler un planeur doit nécessairement descendre.
Voici une
animation Java que
nous avons créée pour mieux comprendre le
phénomène.
Mais
attention, un tel appareil peut aussi monter de ses propres ailes.
C’est le cas
de la voltige. En effet, c’est en réalité le couple
altitude/vitesse qui
constitue le réservoir énergétique du planeur
(comme le sont les cuves à
kérosène d’un airbus...). Si un planeur incline son
nez vers le haut, il génère
plus de portance, prend de l’altitude et donc gagne de
l’énergie potentiel au
déficit de l’énergie cinétique. Il lui
suffit donc de redescendre
pour reprendre de la vitesse.
Voyez
plutôt une vidéo
illustrant ce mécanisme (en
voltige).
Lors de ces
échanges d’énergies, la
traînée consomme toujours autant, seulement elle change sa
source. Le mécanisme
décrit plus haut peut donc être inversée.
Cependant, c’est le seul valable pour
un vol dit stabilisé.
Tout
ceci nous amène à parler de la notion de finesse. La finesse d’un
planeur
représente sa capacité à planer. En effet, cette
caractéristique correspond au
rapport de la distance par l’altitude ou de la vitesse par le
taux de chute, c'est
à dire l'angle de piqué que doit adopter le planeur pour
avoir une trajectoire
rectiligne à vitesse constante. Par exemple, un planeur de
finesse 40 pourra
parcourir, à partir d’une altitude de 1000 mètres,
une distance de 40
kilomètres avant de toucher le sol. En fait, la finesse
dépend de l’aérodynamique
de l’appareil : elle consiste
à générer une portance
optimale pour une traînée la plus réduite possible.

La finesse
d’un planeur.
Ainsi, pour
conclure cette partie, le vol d’un planeur est une
longue glissade silencieuse, une descente lente et
régulière. Cependant un
planeur peut rester en l’air beaucoup plus longtemps. Pour cela,
il suffit de
recharger le réservoir d’énergie potentielle
à l’aide de forces atmosphériques,
et c’est ici que commence véritablement ce qu’on
appelle le « vol à
voile ». Mais comment réussit-il à utiliser
l’énergie de l’environnement
pour reprendre de l’altitude ?
|

 Accueil
Accueil
 Synthèses
personnelles
Synthèses
personnelles  Multimédia
Multimédia
 Glossaire
Glossaire
 Bibliographie
Bibliographie







