Quizz algèbre

QUIZZ ALGÈBRE

LOGIQUE - ENSEMBLES - RELATIONS - ENSEMBLES ORDONNÉS - APPLICATIONS

LOIS DE COMPOSITION INTERNES - GROUPES - ANNEAUX -CORPS - DÉFINITION DU CORPS DES NOMBRES RÉELS

ARITHMÉTIQUE DES ENTIERS - ARITHMÉTIQUE DANS UN ANNEAU

ALGEBRE LINEAIRE : ESPACES VECTORIELS - APPLICATIONS LINEAIRES - MATRICES - MODULES

ALGEBRE BILINEAIRE : FORMES BILINÉAIRES - PRODUITS SCALAIRES, ESPACES PREHILBERTIENS

LOGIQUE

L1 : La négation de A => B est :

1. A => non B 2. non A => non B 3. A et non B 4. non A et non B
réponse

L2 : Si une implication est fausse, sa réciproque est vraie.

L2 : est équivalent à .
réponse

ENSEMBLES

E 1 : .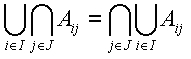

E 2 : .

E3 : .

RELATIONS

R1 : Il suffit pour une relation dans un ensemble d'être transitive et symétrique pour que ce soit une relation d'équivalence.
réponse

ENSEMBLES ORDONNÉS
On considère dans ce qui suit un ensemble E muni d'une relation d'ordre.

O1 : Pour A et B inclus dans E, .

O2 : toute partie non vide majorée de E possède une borne supérieure.

O3 : ne pas avoir de plus grand que soi équivaut à être le plus grand ; autrement dit :

réponse

O4 : toute bijection entre deux ensembles ordonnés est monotone.

O5 : la réciproque d'une bijection croissante est croissante.
réponse

APPLICATIONS

A1 : Si la composée de deux applications est bijective, chacune des applications est bijective.

A2 : Si f est une application de E vers F, A et B deux parties de E, alors .

A3 : Si f est une application de E vers F, A et B deux parties de E, alors .

A4 : S'il existe une injection de A vers B et une injection de B vers A, alors il existe une bijection de A sur B.

A5 : Il n'existe jamais de bijection d'un ensemble sur une de ses parties strictes.

A6 : Un ensemble est infini sss'il 'existe une bijection de l'ensemble sur une de ses parties strictes.

A6 : Il n'existe jamais de bijection d'un ensemble E sur son carré E².

A7 : Un ensemble est infini sss'il 'existe une bijection de l'ensemble sur son carré

A8 : Il n'existe jamais de bijection d'un ensemble sur l'ensemble de ses parties.

LOIS DE COMPOSITION INTERNES

LCI 1 : si une loi possède un élément neutre, un élément ne peut avoir plus d'un symétrique pour cette loi.

LCI 2 : Si A est une partie stable d'un ensemble Epour une loi * définie dans E, et si e est un élément neutre pour * dans E et e' un élément neutre pour la restriction de * à A, alors e = e'.

LCI 3 : si une loi vérifie por tous x,y,z, alors _* est à la fois associative et commutative.F 138

GROUPES

G1 : Un carré latin ayant un élément neutre est un groupe (plus précisément, une loi sur un ensemble fini où tout élément est simplifiable et ayant un élément neutre, est une loi de groupe).

G2 : Un carré latin commutatif ayant un élément neutre est un groupe (plus précisément, une loi commutative sur une ensemble fini où tout élément est simplifiable et ayant un élément neutre, est une loi de groupe).

G : une partie stable d'un groupe qui est un groupe a même élément neutre que le groupe de départ.

Il faut au moins n-1 transpositions pour engendrer Sn. (forum 92)

ANNEAUX

La définition ici choisie des anneaux n'impose pas l'existence d'un élément unité.

A1 : dans un anneau, un élément est simplifiable (ou régulier) pour la multiplication sssi ce n'est pas un diviseur de zéro (un diviseur de zéro est un élément non nul a tel qu'il existe un élément non nul b avec a b = 0).

A : un sous-anneau d'un anneau unitaire qui possède un élément unité, a le même élément unité que l'anneau de départ.

CORPS

C : une partie stable d'un corps (pour les 2 lois) qui est un corps a même élément unité que le corps de départ.

morphisme de corps : forum 97

DÉFINITION DU CORPS DES NOMBRES RÉELS
On rappelle que tous les corps commutatifs totalement ordonnés et complets (toute partie non vide majorée possède une borne supérieure) sont isomorphes ; l'ensemble des nombres réels est l'un d'entre eux.

R1 : Tout corps commutatif peut être totalement ordonné.

R2 : Tout corps commutatif totalement ordonné est une extension d'un corps isomorphe à .

R3 : Deux corps commutatifs totalement ordonnés égaux en tant que corps sont isomorphes en tant qu'ensembles ordonnés.

R4 : Un corps commutatif totalement ordonné où toute suite de Cauchy est convergente est isomorphe à .

R5 : Un corps commutatif totalement ordonné est archimédien ().

R6 : Un corps commutatif totalement ordonné complet (au sens ci-dessus) est archimédien.

R7 : Tout corps commutatif totalement ordonné peut être complété (i.e. est un sous-corps totalement ordonné d'un corps commutatif totalement ordonné complet)

ARITHMÉTIQUE DES ENTIERS

a,b,c,a',a" désignent des entiers, n un entier naturel.

AR : Si a divise bc et a ne divise pas b, alors a divise c.

AR : a divise bc équivaut à ce que a = a' a" avec a' divise b et a'' divise c.

AR : pgcd(a, b) = pgcd(a + b, a - b).

AR : pgcd(a, b) = pgcd(a + b, ab).

AR : S’il existe u et v entiers tels que au + bv = c alors pgcd(a, b) = c.

AR : « a et b premiers entre eux » équivaut à « ppcm(a, b) = |ab| ».

AR : trois entiers premiers dans leur ensemble sont premiers entre eux deux à deux.

AR : p premier implique 2^p- 1 premier

AR : n divise 2^n-1- 1 entraîne n premier

AR : n divise a^n-1- 1 pour tout a entraîne n premier

AR : n divise a^n-1- 1 pour tout a premier avec n entraîne n premier

Le produit de n entiers consécutifs est divisible par n!

Parmi n entiers consécutifs, il en existe au moins un qui est premier avec les autres. (forum 35)

Parmi 2n - 1 entiers, on peut toujours en trouver n dont la somme est divisible par n. (se)

algo glouton forum 95

ARITHMÉTIQUE DANS LES ANNEAUX

Dans un anneau commutatif unitaire, il y a équivalence entre
(1) x divise y et y divise x
(2) il existe u inversible tel que y=ux. (forum 75)

ALGEBRE LINEAIRE

ESPACES VECTORIELS

EV : Une partie d'un espace vectoriel E telle que l'ensemble des différences de ses éléments est un sous-espace vectoriel de E est un sous-espace affine de E.

La réunion de deux sous-espaces vectoriels distincts n'est jamais un sous-espace vectoriel.

Un espace vectoriel ne peut être réunion de deux de ses sous-espaces vectoriels stricts.

Un espace vectoriel ne peut être réunion d'un nombre fini de ses sous-espaces vectoriels stricts.

Un espace vectoriel sur un corps infini ne peut être réunion d'un nombre fini de ses sous-espaces vectoriels stricts. (forum 105)

APPLICATIONS LINEAIRES

La somme de l'image et du noyau d'un endomorphisme d'un espace E est égale à E.

Un endomorphisme injectif est forcément surjectif.

Un endomorphisme surjectif est forcément injectif.

Un endomorphisme f est simplifiable à gauche dans L(E) sss'il est injectif.

Un endomorphisme f est simplifiable à droite dans L(E) sss'il est surjectif.

Si F est un sous-espace vectoriel stable par un automorphisme f d'un espace vectoriel E (i.e. ), alors F est globalement invariant (). forum 85

Un endomorphisme d'un espace vectoriel complexe a toujours au moins une valeur propre.

L'ensemble des valeurs propres d'un endomorphisme réel est discret.

Si f et g sont deux endomorphismes d'un espace vectoriel de dimension finie, ils ont le même polynôme carctéristique.

Si f et g sont deux endomorphismes d'un espace vectoriel de dimension finie, ils ont le même polynôme minimal (13).

MATRICES

Deux matrices ayant les mêmes polynômes caractéristiques et les m^mes polynomes minimaux sont semblables (43)

Toute matrice est somme de 2 matrices diagonalisables (forum 42)

Une matrice sans valeur propre est inversible

MODULES

ALGEBRE BILINEAIRE

FORMES BILINÉAIRES

Toute forme bilinéaire antisymétrique () est alternée ().

La restriction d'une forme quadratique non dégénérée à un sous-espace vectoriel non nul est non nulle.

Deux sous-espaces vectoriels orthogonaux pour une forme quadratique sont distincts.

Deux formes quadratiques ont toujours une base de diagonalisation commune.

Deux formes quadratiques d'un espace vectoriel réel ont la même signature sss'il existe deux bases dans lesquelles elles ont la même matrice.

PRODUITS SCALAIRES, ESPACES PREHILBERTIENS

Une forme bilinéaire symétrique définie (i.e. sans vecteur isotrope) est un produit scalaire ou l'opposé d'un produit scalaire.

Les similitudes d'un espace préhilbertien (i.e. vérifiant ) sont les endomorphismes non nuls conservant l'orthogonalité (i.e. vérifiant ) forum 86

Une application d'un espace préhibertien dans lui-même conservant l'orthogonalité est une similitude.

forum 99

F 132

P age perso de l'auteur page principale algèbre suites et séries fonctions topologie géométrie autres